(本小题满分12分)有一种新型的洗衣液,去污速度特别快.已知每投放 且
且 个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度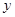 (克/升)随着时间
(克/升)随着时间 (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为 ,其中
,其中 .根据经验,当水中洗衣液的浓度不低于
.根据经验,当水中洗衣液的浓度不低于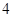 (克/升)时,它才能起到有效去污的作用.
(克/升)时,它才能起到有效去污的作用.
(Ⅰ)若投放 个单位的洗衣液,
个单位的洗衣液, 分钟时水中洗衣液的浓度为
分钟时水中洗衣液的浓度为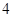 (克/升),求
(克/升),求 的值 ;
的值 ;
(Ⅱ)若投放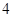 个单位的洗衣液,则有效去污时间可达几分钟?
个单位的洗衣液,则有效去污时间可达几分钟?
如图,平面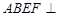 平面
平面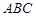 ,四边形
,四边形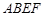 为矩形,
为矩形,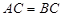 .
.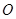 为
为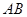 的中点,
的中点,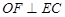 .
.
(1)求证: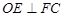 ;
;
(2)若 时,求二面角
时,求二面角 的余弦值.
的余弦值.
我国政府对PM2.5采用如下标准:
| PM2.5日均值m(微克/立方米) |
空气质量等级 |
 |
一级 |
 |
二级 |
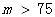 |
超标 |
某市环保局从180天的市区PM2.5监测数据中,随机抽取l0天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
(1)求这10天数据的中位数.
(2)从这l0天的数据中任取3天的数据,记 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求 的分布列;
的分布列;
(3)以这10天的PM2.5日均值来估计这180天的空气质量情况,其中大约有多少天的空气质量达到一级.
某同学用“五点法”画函数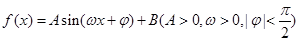 在某一个周期内的图象时,列表并填入的部分数据如下表:
在某一个周期内的图象时,列表并填入的部分数据如下表:
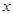 |
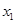 |
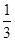 |
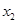 |
 |
 |
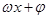 |
 |
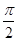 |
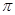 |
 |
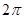 |
 |
 |
 |
 |
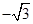 |
 |
(1)请求出上表中的 ,并直接写出函数
,并直接写出函数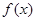 的解析式;
的解析式;
(2)将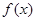 的图象沿
的图象沿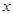 轴向右平移
轴向右平移 个单位得到函数
个单位得到函数 ,若函数
,若函数 在
在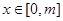 (其中
(其中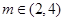 )上的值域为
)上的值域为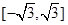 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为 ,求
,求 与
与 夹角
夹角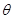 的大小。
的大小。
已知:0<a<b<c<d 且a+d=b+c,求证: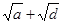 <
< 
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 |
2004 |
2006 |
2008 |
2010 |
2012 |
| 需求量(万吨) |
236 |
246 |
257 |
276 |
286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程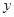 =
=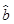 x+
x+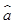
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.