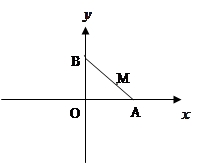(本小题满分15分)平面直角坐标系xOy中,已知以M为圆心的圆M经过点F1(0,-c),F2(0,c),A(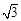 c,0)三点,其中c>0.
c,0)三点,其中c>0.
(1)求圆M的标准方程(用含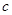 的式子表示);
的式子表示);
(2)已知椭圆 (其中
(其中 )的左、右顶点分别为D、B,圆M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
)的左、右顶点分别为D、B,圆M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
斜率为2的直线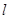 经过抛物线
经过抛物线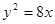 的焦点
的焦点 ,且与抛物线相交于
,且与抛物线相交于 两点,求线段
两点,求线段 的长。
的长。
已知函数 .
.
(1)求函数的单调区间;
(2)若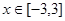 ,试求函数在此区间上的最大值与最小值.
,试求函数在此区间上的最大值与最小值.
求双曲线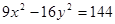 的实轴长、虚轴长、焦点坐标、离心率、渐近线方程。
的实轴长、虚轴长、焦点坐标、离心率、渐近线方程。
(1).已知抛物线的焦点是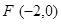 ,求它的标准方程;
,求它的标准方程;
(2).已知椭圆的长轴长是短轴长的3倍,且经过点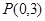 ,求椭圆的标准方程;
,求椭圆的标准方程;
(3).已知双曲线两个焦点分别为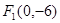 ,
,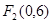 ,双曲线上一点
,双曲线上一点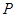 到
到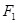 ,
,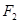 的距离差的绝对值等于8, 求双曲线的方程.
的距离差的绝对值等于8, 求双曲线的方程.
如图,线段AB的两个端点A、B分别在x轴,y轴上滑动,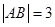 ,点M是线段AB上一点,且
,点M是线段AB上一点,且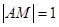 点M随线段AB的滑动而运动.
点M随线段AB的滑动而运动.
(I)求动点M的轨迹E的方程
(II)过定点N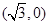 的直线
的直线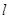 交曲线E于C、D两点,交y轴于点P,若
交曲线E于C、D两点,交y轴于点P,若 的值
的值