已知半径为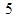 的圆的圆心M在
的圆的圆心M在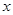 轴上,圆心M的横坐标是整数,且圆M与直线
轴上,圆心M的横坐标是整数,且圆M与直线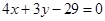 相切.
相切.
求:(Ⅰ)求圆M的方程;
(Ⅱ)设直线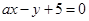 与圆M相交于
与圆M相交于 两点,求实数
两点,求实数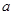 的取值范围.
的取值范围.
某医院有内科医生12名,外科医生8名,现选派5名参加赈灾医疗队,其中
(1)某内科医生甲与某外科医生乙必须参加,共有多少种不同选法?
(2)甲、乙均不能参加,有多少种选法?
(3)甲、乙两人至少有一人参加,有多少种选法?
(4)队中至少有一名内科医生和一名外科医生,有几种选法?
六人按下列要求站一横排,分别有多少种不同的站法?
(1)甲不站两端;
(2)甲、乙必须相邻;
(3)甲、乙不相邻;
(4)甲、乙之间间隔两人;
(5)甲、乙站在两端;
(6)甲不站左端,乙不站右端.
将3种作物种植在如图所示的5块试验田里,每块种植一种作物且相邻的试验田不能种植同一种作物,不同的种植方法共有多少种?
在平面直角坐标系内,点P(a,b)的坐标满足a≠b,且a,b都是集合{1,2,3,4,5,6}的元素,又点P到原点的距离|OP|≥5.求这样的点P的个数.
某体育彩票规定:从01到36共36个号中抽出7个号为一注,每注2元.某人想先选定吉利号18,然后从01至17中选3个连续的号,从19至29中选2个连续的号,从30至36中选1个号组成一注.若这个人要把这种要求的号全买下,至少要花多少元钱?