(本小题满分14分)根据如图所示的程序框图,将输出a,b的值依次分别记为a1,a2, ,an, ,a2008;b1,b2, ,bn, ,b2008.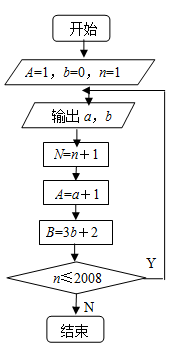
(Ⅰ)求数列 { an } 的通项公式;
(Ⅱ)写出b1,b2,b3,b4,由此猜想{ bn }的通项公式,并证明你的证明;
(Ⅲ)在 ak 与 ak+1 中插入bk+1个3得到一个新数列 { cn } ,设数列 { cn }的前n项和为Sn,问是否存在这样的正整数m,使数列{ cn }的前m项的和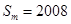 ,如果存在,求出m的值,如果不存在,请说明理由.
,如果存在,求出m的值,如果不存在,请说明理由.
已知圆的方程x2+y2=25,点A为该圆上的动点,AB与x轴垂直,B为垂足,点P分有向线段BA的比λ=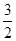 ,
,
(1)求点P的轨迹方程并化为标准方程形式;
(2)写出轨迹的焦点坐标和准线方程。
解不等式:(1)log 2 ≤0.
≤0.
(2)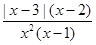 ≥0
≥0
已知函数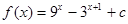 (其中
(其中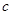 是常数).
是常数).
(1)若当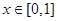 时,恒有
时,恒有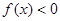 成立,求实数
成立,求实数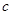 的取值范围;
的取值范围;
(2)若存在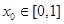 ,使
,使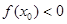 成立,求实数
成立,求实数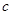 的取值范围;
的取值范围;
甲、乙两地相距12km.A车、B车先后从甲地出发匀速驶向乙地.A车从甲地到乙地需行驶15min;B车从甲地到乙地需行驶10min.若B车比A车晚出发2min:
(1)分别写出A、B两车所行路程关于A车行驶时间的函数关系式;
(2) A、B两车何时在途中相遇?相遇时距甲地多远?
(1)已知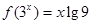 ,求
,求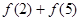 的值;
的值;
(2)若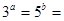
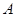
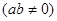 ,且
,且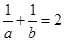 ,求
,求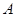 的值.
的值.