(本小题满分12分)如图,四棱锥S一ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC= ,SA=SC=SD=2.
,SA=SC=SD=2.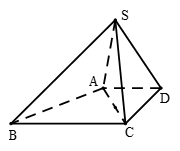
(Ⅰ)求证:AC⊥SD;
(Ⅱ)求二面角A - SB -C的余弦值.
集合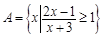 ,
,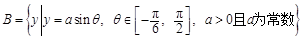 .
.
(1)求集合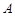 和B;
和B;
(2)若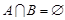 ,求
,求 的取值范围
的取值范围
已知
(1)求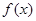 的周期,并求
的周期,并求 时的单调增区间.
时的单调增区间.
(2)在△ABC中,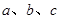 分别是角A,B,C所对的边,若
分别是角A,B,C所对的边,若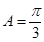 ,且
,且 ,求
,求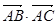 的最大值.
的最大值.
已知抛物线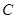 的方程为
的方程为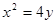 ,直线
,直线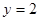 与抛物线
与抛物线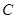 相交
相交
于 两点,点
两点,点 在抛物线
在抛物线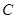 上.(Ⅰ)若
上.(Ⅰ)若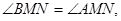 求证:直线
求证:直线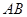
的斜率为定值;
(Ⅱ)若直线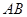 的斜率为
的斜率为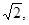 且点
且点 到 直线
到 直线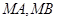 的距离的和为
的距离的和为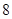 ,试判断
,试判断 的形状,并证明你的结论.
的形状,并证明你的结论.
已知函数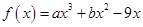 在
在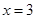 处取得极大值
处取得极大值 .
.
(Ⅰ)求 在区间
在区间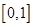 上的最大值;
上的最大值;
(Ⅱ)若过点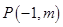 可作曲线
可作曲线 的切线有三条,求实数
的切线有三条,求实数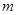 的取值范围.
的取值范围.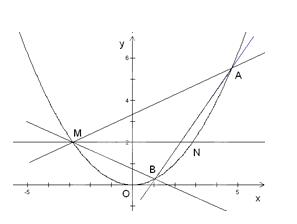
对于给定数列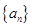 ,如果存在实常数
,如果存在实常数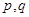 ,使得
,使得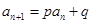 对于任意
对于任意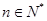 都成立,我们称数列
都成立,我们称数列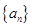 是 “
是 “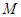 类数列”.
类数列”.
(Ⅰ)已知数列 是 “
是 “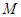 类数列”且
类数列”且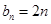 ,求它对应的实常数
,求它对应的实常数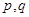 的值;
的值;
(Ⅱ)若数列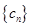 满足
满足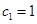 ,
,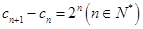 ,求数列
,求数列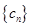 的通项公式.并判断
的通项公式.并判断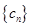 是否为“
是否为“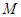 类数列”,说明理由.
类数列”,说明理由.