（本小题满分12分）设函数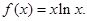
（Ⅰ）设
，讨论函数F（x）的单调性；
（Ⅱ）过两点
的直线的斜率为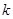
，求证：
已知数列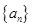
满足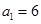
，
；
（1）求数列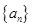的通项公式；
（2）求数列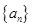的前
项和
，并求当最大时序号的值.
在锐角
中，角
的对边分别是
，且
（1）确定角
的大小：
（2）若
,且
，求的面积.
如图，A，B是海面上位于东西方向相距
海里的两个观测点，现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距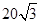
海里的C点的救援船立即即前往营救，其航行速度为30海里/小时，该救援船到达D点需要多长时间？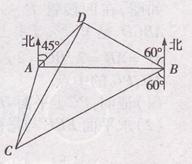
（1）已知等差数列
中
，
，求的公差
；
（2）有三个数成等比数列，它们的和等于14，它们的积等于64，求该数列的公比
.
在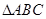
中,角
的对边分别是
，若角成等差数列.
（1）求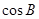
的值；
（2）边成等比数列,求
的值.