因式分解
(1) (2)
(2)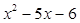
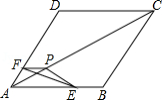
如图,把 放置在菱形 中,使得顶点 , , 分别在线段 , , 上,已知 , , ,且 .
(1)求 的大小;
(2)若 ,求 的值;
(3)若 的三个顶点 、 、 分别在线段 、 、 上运动,请直接写出 长的最大值和最小值.
如图,在矩形 中, , , 是 上的一个动点 不与 , 重合),过点 的反比例函数 的图象与 边交于点 .
(1)当 为 的中点时,求该函数的解析式;
(2)当 为何值时, 的面积最大,最大面积是多少?

小军同学在学校组织的社会实践活动中,负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位: ),并绘制了样本的频数分布表:
|
月均用水量 |
|
|
|
|
|
|
|
|
频数 |
2 |
12 |
① |
10 |
② |
3 |
2 |
|
百分比 |
|
|
|
|
③ |
|
|
(1)请根据题中已有的信息补全频数分布:① ,② ,③ ;
(2)如果家庭月均用水量在 范围内为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)记月均用水量在 范围内的两户为 , ,在 范围内的3户 、 、 ,从这5户家庭中任意抽取2户,试完成下表,并求出抽取出的2户家庭来自不同范围的概率.
|
|
|
|
|
|
|
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
表示 边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么 与 的关系式是: (其中 , 是常数,
(1)通过画图,可得:四边形时, ;五边形时,
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求 , 的值.
先化简,再求值: ,其中 是方程 的解.