已知:把Rt△ABC和Rt△DEF按如图甲摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠BAC = ∠DEF = 90°,∠ABC = 45°,BC =" 9" cm,DE =" 6" cm,EF =" 8" cm.
如图乙,△DEF从图甲的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△DEF的顶点F出发,以3 cm/s的速度沿FD向点D匀速移动.当点P移动到点D时,P点停止移动,△DEF也随之停止移动.DE与AC相交于点Q,连接BQ、PQ,设移动时间为t(s).解答下列问题:设三角形BQE的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围;
当t为何值时,三角形DPQ为等腰三角形?
是否存在某一时刻t,使P、Q、B三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由


按右图的流程,输入一个数据x,根据y与x的函数关系式就 输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20到100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(ⅰ)、新数据都在60到100(含60和100)之间。
(ⅱ)、新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。问:若y与x的关系式是 y=x+p(100-x),请说明:当p=
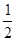 时,这种变换满足上述两个要求。
时,这种变换满足上述两个要求。若按关系式:y=a(x-h)2+k(a﹥0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要求写出关系式得出的主要过程)

如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P. 设∠BPC=α,如果sinα是方程5x-13x+6=0的根,求cosα的值;
在(1)的条件下,求弦CD的长.

据2010年5月8日《杭州日报》报道:今年“五一”黄金周期间,我市实现旅游收入再创历史新高,旅游消费呈现多样化,各项消费所占的比例如图秘所示,其中住宿消费为3438.24万元.求我市今年“五一”黄金周期间旅游消费共多少亿元?旅游消费中各项消费的中位数是多少万元?
对于“五一”黄金周期间的旅游消费,如果我市2012年要达到3.42亿元的目标,那么,2010年到2012年的平均增长率是多少?
2010年杭州市“五一”黄金周旅游各项消费分布统计图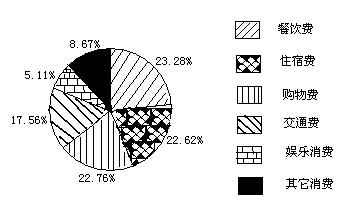
如图,已知抛物线 经过点
经过点 ,抛物线的顶点为
,抛物线的顶点为 ,过
,过 作射线
作射线 .过顶点
.过顶点 平行于
平行于 轴的直线交射线
轴的直线交射线 于点
于点 ,
, 在
在 轴正半轴上,连结
轴正半轴上,连结 .
.求该抛物线的解析式;
动点
 从点
从点 出发,以每秒1个长度单位的速度沿射线
出发,以每秒1个长度单位的速度沿射线 运动,设点
运动,设点 运动的时间为
运动的时间为 .问当
.问当 为何值时,四边形
为何值时,四边形 分别为平行四边形?直角梯形?等腰梯形?
分别为平行四边形?直角梯形?等腰梯形?若
 ,动点
,动点 和动点
和动点 分别从点
分别从点 和点
和点 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿
同时出发,分别以每秒1个长度单位和2个长度单位的速度沿 和
和 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
 ,连接
,连接 ,当
,当 为何值时,四边形
为何值时,四边形 的面积最小?并求出最小值及此时
的面积最小?并求出最小值及此时 的长.
的长.