(本题10分)如图,是由一些棱长都为1的小正方体组合成的简单几何体. 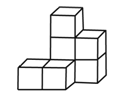
(1)该几何体的表面积(含下底面)为 ;
(2)请画出这个几何体的三视图并用阴影表示出来;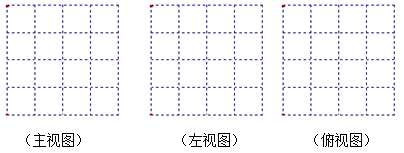
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
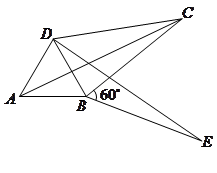
如图:△ABC和△ADE是等边三角形,证明:BD=CE.
 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
(1)作出与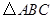 关于
关于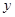 轴对称的
轴对称的 ;并写出A1、B1、C1坐标。
;并写出A1、B1、C1坐标。
(2)将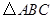 向下平移3个单位长度,画出平移后的
向下平移3个单位长度,画出平移后的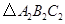
先化简,再求值: ,其中
,其中 ,
,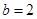 .
.
已知正方形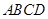 中,
中, 绕点
绕点 沿顺时针方向旋转,它的
沿顺时针方向旋转,它的
两边分别交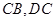 (或它们的延长线)于点
(或它们的延长线)于点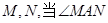 绕点
绕点 旋转到
旋转到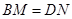 时(如图28①),易证
时(如图28①),易证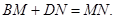

(1)当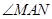 绕点
绕点 旋转到
旋转到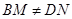 时(如图28②),线段
时(如图28②),线段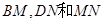 之间有怎样的数量关系?写出猜想,并加以证明;
之间有怎样的数量关系?写出猜想,并加以证明;
(2)当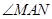 绕点
绕点 旋转到如图28③所示的位置时,线段
旋转到如图28③所示的位置时,线段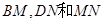 之间又有怎样的数量关系?请直接写出你的猜想.(9分)
之间又有怎样的数量关系?请直接写出你的猜想.(9分)
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称_______,___;
(2)如图,已知格点(小正方形的顶点) ,
,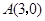 ,
,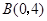 ,请你直接写出所有以格点为顶点,
,请你直接写出所有以格点为顶点, 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形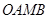 的顶点M的坐标。
的顶点M的坐标。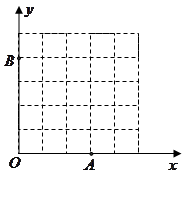
(3)如图,将 绕顶点
绕顶点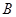 按顺时针方向旋转
按顺时针方向旋转 ,得到
,得到 ,连结
,连结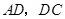 ,
,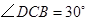 .求证:
.求证: ,即四边形
,即四边形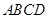 是勾股四边形.
是勾股四边形.