某班元旦迎新有奖活动中有一节目，参与者同时掷出三个各面分别标有数字1,2,3,4且质地均匀的小正四面体，规定：每位参与者只掷依次，选取着地一面的数字，如果掷出所取的三个数字都不相同，如“1、2、3”，“1、2、4”等情形为获奖.
（1）求参与者获奖的概率；
（2）获奖一次得到十元的奖品，否则得到纪念奖2元的奖品.求甲、乙两位参与者总的奖品金额恰为12元的概率.
(本小题满分14分)已知函数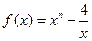
，且
.
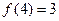(1)判断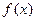
的奇偶性并说明理由；
(2)判断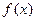在区间
上的单调性，并证明你的结论；
(3)若在区间
上，不等式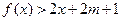
恒成立，试确定实数
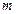的取值范围.
(本小题满分14分)如图在底面是矩形的四棱锥P-ABCD中，PA⊥底面ABCD， E、F分别是PC、PD的中点，求证：（1）EF∥平面PAB；
（2）平面PAD⊥平面PDC．
(本小题满分14分)已知集合A={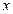
︱3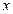＜≤7},B={x︱2<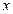<10},C={︱<
}
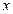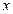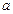⑴ 求A∪B，(CuA)∩B
⑵ 若A∩C≠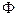
，求a的取值范围
(本题满分13分)
已知函数
在
上是减函数，在
上是增函数，函数
在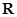
上有三个零点．
（1）求
的值；
（2）若1是其中一个零点，求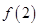
的取值范围；
（3）若
，试问过点（2，5）可作多少条直线与曲线y=g(x)相切？请说明理由。
(本题满分13分)
对于给定数列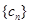
，如果存在实常数
使得
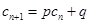对于任意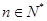
都成立，我们称数列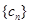是 “M类数列”．
（1）若
，
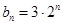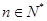，，数列
、
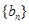是否为“M类数列”？若是，指出它对应的实常数
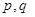，若不是，请说明理由；
（2）证明：若数列是“M类数列”，则数列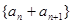
也是“M类数列”；
（3）若数列满足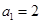
，
，
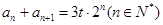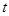为常数．求数列前
项的和．