某公司计划2015年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元。甲、乙电视台的广告收费标准分别为
元/分钟和200元/分钟。假定甲、乙两个电视台为该公司所做的每分钟广告，能给公司带来的收益分别为0.3万元和0.2万元。问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？
（本小题满分10分）已知在半径为10的圆O中，弦AB的长为10。
（1）求弦AB所对的圆心角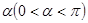
的大小。
（2）求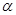
所在的扇形弧长
及弧所在的弓形的面积S。
已知椭圆
的离心率为
，且过点
（1）求椭圆的标准方程：
（2）四边形ABCD的顶点在椭圆上，且对角线AC，BD过原点O，若
①求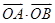
的最值：
②求证：四边形ABCD的面积为定值.
已知圆A：x2＋y2－2x－2y－2＝0.
（1）若直线l：ax＋by－4＝0平分圆A的周长，求原点O到直线l的距离的最大值；
（2）若圆B平分圆A的周长，圆心B在直线y＝2x上，求符合条件且半径最小的圆B的方程．
如图，将边长为2，有一个锐角为60°的菱形
，沿着较短的对角线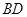
对折，使得
，
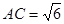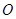为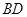的中点.若P为AC上的点，且满足
。
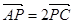（Ⅰ）求证：
（Ⅱ）求三棱锥
的体积；
平面内动点
到定点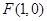
的距离比它到
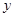轴的距离大
。
（1）求动点
的轨迹
的方程；
（2）已知点A（3,2）, 求
的最小值及此时P点的坐标．