设函数,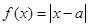
(1)当 ,解不等式,
,解不等式,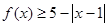 ;
;
(2)若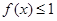 的解集为
的解集为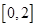 ,
,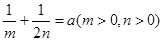 ,求证:
,求证: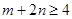
已知函数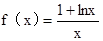
若函数在区间(a,a+ )上存在极值,其中a>0,求实数a的取值范围;
)上存在极值,其中a>0,求实数a的取值范围;
如果当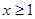 时,不等式
时,不等式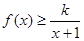 恒成立,求实数
恒成立,求实数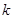 的取值范围。
的取值范围。
如图,椭圆C方程为 (
(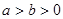 ),点
),点 为椭圆C的左、右顶点。
为椭圆C的左、右顶点。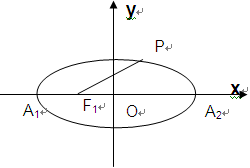
(1)若椭圆C上的点到焦点的距离的最大值为3,最小值为1,求椭圆的标准方程;
(2)若直线 与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足
与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足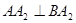 ,求证:直线
,求证:直线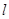 过定点,并求出该点的坐标。
过定点,并求出该点的坐标。
(本小题满分12分)
如图:直三棱柱ABC—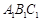 中,
中,
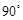 ,
, 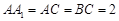 ,D为AB中点。
,D为AB中点。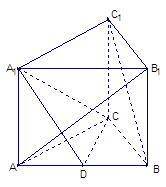
(1)求证: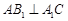 ;
;
(2)求证: ∥平面
∥平面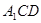 ;
;
(3)求C1到平面A1CD的距离。
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4,
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率。
在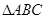 中
中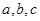 分别为A,B,C所对的边,
分别为A,B,C所对的边,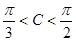 且
且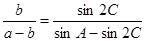
(1)判断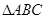 的形状;
的形状;
(2)若
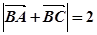 ,求
,求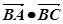 的取值范围
的取值范围