《科学》介绍了一种新技术——航天飞缆,航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统。飞缆系统在太空飞行中能为自身提供电能和拖曳力,它还能清理“太空垃圾”等。该系统的工作原理可用物理学的基本定律来解释。
下图为飞缆系统的简化模型示意图,图中两个物体P,Q的质量分别为mP、mQ,柔性金属缆索长为l,外有绝缘层,系统在近地轨道作圆周运动,运动过程中Q距地面高为h。设缆索总保持指向地心,P的速度为vP。已知地球半径为R,地面的重力加速度为g。
(1)飞缆系统在地磁场中运动,地磁场在缆索所在处的磁感应强度大小为B,方向垂直于纸面向外。设缆索中无电流,求缆索P、Q哪端电势高?两端的电势差多大?
(2)设缆索的电阻为R1,如果缆索两端物体P、Q通过周围的电离层放电形成电流,相应的电阻为R2,求缆索所受的安培力多大?
(3)求缆索对Q的拉力FQ多大?
如图所示,一质量M=2.0kg的长木板AB静止在水平面上,木板的左侧固定一半径R=0.60m的四分之一圆弧形轨道,轨道末端的切线水平,轨道与木板靠在一起,且末端高度与木板高度相同。现在将质量m=l.0kg的小铁块(可视为质点)从弧形轨道顶端由静止释放,小铁块到达轨道底端时的速度v0=3.0m/s,最终小铁块和长木板达到共同速度。忽略长木板与地面间的摩擦。取重力加速度g=l0m/s2。求
(1)小铁块在弧形轨道末端时所受支持力的大小F;
(2)小铁块在弧形轨道上滑动过程中克服摩擦力所做的功Wf;
(3)小铁块和长木板达到的共同速度v。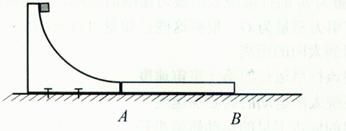
如图所示, A、B两物体的质量都为m,拉A物体的细线与水平方向的夹角为30°时处于静止状态,不考虑摩擦力,设弹簧的劲度系数为k.若悬线突然断开后,A在水平面上做周期为T的简谐运动,当B落地时,A恰好将弹簧压缩到最短,求: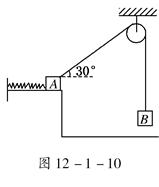
(1)A振动时的振幅;
(2)B落地时的速度.
如图甲所示是一个单摆振动的情形,O是它的平衡位置,B、C是摆球所能到达的最远位置.设摆球向右方向运动为正方向.图乙所示是这个单摆的振动图象.根据图象回答:(取π2=10)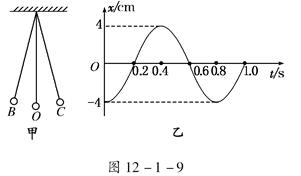
(1)单摆振动的频率是多大?
(2)开始时刻摆球在何位置?
(3)若当地的重力加速度为10 m/s2,试求这个摆的摆长是多少?
如图所示是某同学设计的测量物体质量的装置,其中P是光滑水平面,N是质量为M的带夹子的金属盒,金属盒两端分别连接轻质弹簧;Q是固定于盒子上的遮光片,利用它和光电计时器能测量金属盒振动时的频率.已知弹簧振子做简谐运动时的周期T=2π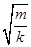 ,其中m是振子的质量,k 是常数.当空盒振动时,测得振动频率为f1;把一物体夹在盒中,并使其振动时,测得频率为f2.你认为这套装置能测量物体的质量吗?如果不能,请说明理由;若能,请求出被测物体的质量.
,其中m是振子的质量,k 是常数.当空盒振动时,测得振动频率为f1;把一物体夹在盒中,并使其振动时,测得频率为f2.你认为这套装置能测量物体的质量吗?如果不能,请说明理由;若能,请求出被测物体的质量.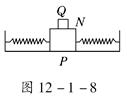
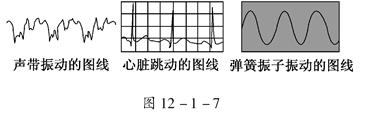
如图所示的三个图线分别是用不同的传感器测出的不同物体的振动图线.从三个图线可知,这三个物体振动的共同特点是具有________;三个物体中,最简单的振动是________的振动;图中心脏跳动的图线是某人的心电图,方格纸每个小方格的宽度是0.5 cm,心电图记录仪拖动方格纸的速度是1.8 cm/s,则此人的心率是________次/分.