(本小题满分12分)设全集为R,集合 ,
, ,
,
(1)求: ;
;
(2)若集合 ,满足
,满足 ,求实数
,求实数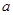 的取值范围。
的取值范围。
(本小题满分12分)
已知函数 ,
, (其中
(其中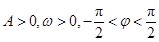 ),其部分图
),其部分图
像如图5所示.
(1)求函数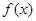 的解析式;
的解析式;
(2)已知横坐标分别为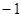 、
、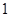 、
、 的三点
的三点 、
、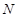 、
、 都在函数
都在函数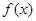 的图像上,求
的图像上,求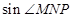 的值.
的值.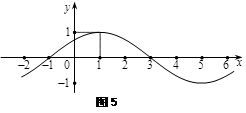
(几何证明选讲选做题)如图4, 是圆
是圆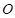 上的两点,且
上的两点,且 ,
, ,
, 为
为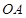 的中点,连接
的中点,连接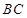 并延长交圆
并延长交圆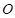 于点
于点 ,则
,则 .
.
已知等比数列 的首项
的首项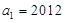 ,公比
,公比 ,数列
,数列 前n项和记为
前n项和记为 ,前n
,前n
项积记为 .
.
(Ⅰ)求数列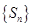 的最大项和最小项;
的最大项和最小项;
(Ⅱ)判断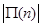 与
与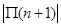 的大小, 并求
的大小, 并求 为何值时,
为何值时, 取得最大值;
取得最大值;
(Ⅲ)证明 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
些等差数列的公差按从小到大的顺序依次设为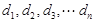 ,证明:数列
,证明:数列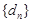 为等比数列。
为等比数列。
(参考数据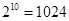 )
)
(本小题满分14分) 已知函数 ,且函数
,且函数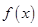 是
是 上的增函数。
上的增函数。
(1)求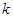 的取值范围;
的取值范围;
(2)若对任意的 ,都有
,都有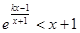 (e是自然对数的底),求满足条件的最大整数
(e是自然对数的底),求满足条件的最大整数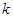
的值。
.(本小题满分14分)
已知椭圆 、抛物线
、抛物线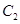 的焦点均在
的焦点均在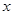 轴上,
轴上, 的中心和
的中心和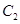 的顶点均为原点
的顶点均为原点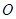 ,从每条曲
,从每条曲
线上取两个点,将其坐标记录于下表中:
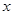 |
3 |
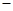 2 2 |
4 |
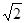 |
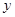 |
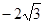 |
0 |
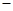 4 4 |
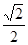 |
(Ⅰ)求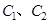 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线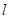 满足条件:①过
满足条件:①过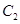 的焦点
的焦点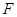 ;②与
;②与 交不同两点
交不同两点 且满
且满
足 ?若存在,求出直线
?若存在,求出直线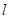 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。