如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若DE=
，∠DPA=45°．
（1）求⊙O的半径；
（2）求图中阴影部分的面积.
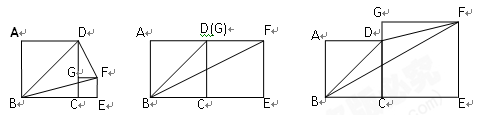
正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上. 分别连接BD，BF，FD，得到△BFD. （1）在图中，若正方形CEFG的边长分别为1，3，4，且正方形ABCD的边长均为3，请通过计算填写下表：
正方形CEF G的边长 |
1 |
3 |
4 |
| △BFD的面积 |
（2）若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S△BFD的大小，并结合图证明你的猜想.
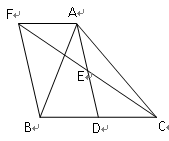
如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于F，且AF=BD，连接BF.（1）求证：D是BC的中点.
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论.
(8分)观察下列各式及验证过程：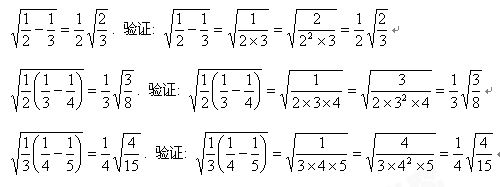
（1）按照上述三
个等式及其验证过程的基本思路，猜想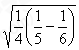
的变形结果并进行验证；（2）针对上述各式反映的规律，写出用n（
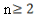的自然数）表示的等式，并进行验证.
(10分)如图，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE，GC.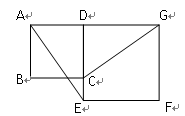
（1）试猜想AE与GC有怎样的位置关系，并证明你的结论；
（2）将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图，连接AE和GC. 你认为（1）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由.
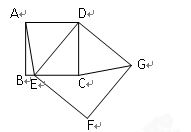
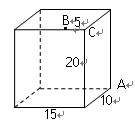
(8分)如图,长方体的长为15，宽为10，高为20，点B离点C的距离是5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？