已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.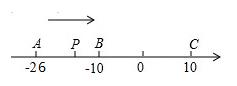
(1)用含t的代数式表示P到点A和点C的距离:PA=________,PC=_____________
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回点A,当点Q开始运动后,请用t的代数式表示P、Q两点间的距离。(友情提醒:注意考虑P、Q的位置)
(·湖南常德)已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF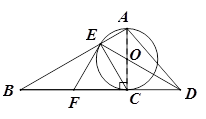
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
(·湖北孝感)如图, 为⊙O的直径,
为⊙O的直径, 是
是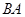 延长线上一点,
延长线上一点,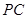 切⊙O于点
切⊙O于点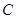 ,
,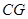 是⊙O的弦,
是⊙O的弦,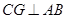 ,垂足为
,垂足为 .
.
(1)求证: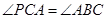 ;
;
(2)过点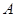 作
作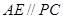 交⊙O于点
交⊙O于点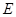 ,交
,交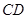 于点
于点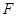 ,连接
,连接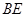 .若
.若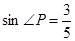 ,
,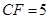 ,求
,求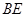 的长.
的长.
(·湖北孝感) 如图,一条公路的转弯处是一段圆弧(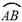 ).
).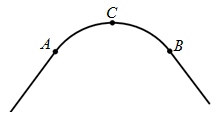
(1)用直尺和圆规作出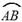 所在圆的圆心
所在圆的圆心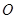 ;(要求保留作图痕迹,不写作法)
;(要求保留作图痕迹,不写作法)
(2)若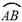 的中点
的中点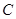 到弦
到弦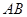 的距离为
的距离为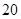 m,
m,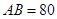 m,求
m,求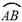 所在圆的半径.
所在圆的半径.
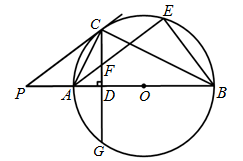
(·湖北襄阳,25题)如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.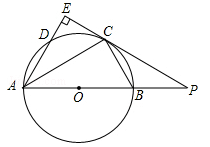
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
(·湖北武汉,21题,分)(本题8分)如图,AB是⊙O的直径,∠ABT=45°,AT=AB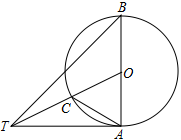
(1)求证:AT是⊙O的切线
(2)连接OT交⊙O于点C,连接AC,求tan∠TAC的值