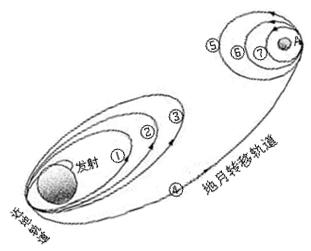
电阻可忽略的光滑平行金属导轨长S=1.15m,两导轨间距L="0.75" m,导轨倾角为30°,导轨上端ab接一阻值R=1.5Ω的电阻,磁感应强度B=0.8T的匀强磁场垂直轨道平面向上。阻值r=0.5Ω,质量m=0.2kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热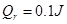 。(取
。(取 )求:
)求:
(1)金属棒在此过程中克服安培力的功 ;
;
(2)金属棒下滑速度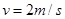 时的加速度
时的加速度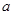 .
.
(3)为求金属棒下滑的最大速度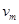 ,有同学解答如下:由动能定理
,有同学解答如下:由动能定理 ,……。由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答。
,……。由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答。
如图所示,倾角q=30°、宽度L=1.0m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1.0T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上,现用一平行导轨的牵引力牵引一根质量m=0.20kg、电阻R=1.0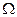 、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦)。若牵引力功率恒为72W,经时间t=2.0s达到稳定速度,此过程金属棒向前滑行的位移S=4.0m。求金属棒的稳定速度及此过程金属棒上产生的热量(结果保留两位有效数字)。
、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦)。若牵引力功率恒为72W,经时间t=2.0s达到稳定速度,此过程金属棒向前滑行的位移S=4.0m。求金属棒的稳定速度及此过程金属棒上产生的热量(结果保留两位有效数字)。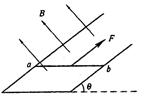
如图所示,虚线和实线分别为一列简谐横波上两质点P、Q的振动图象,两质点相距30m,则(1)若P质点离波源近,则波速多大?(2)若Q质点离波源近,则波速多大?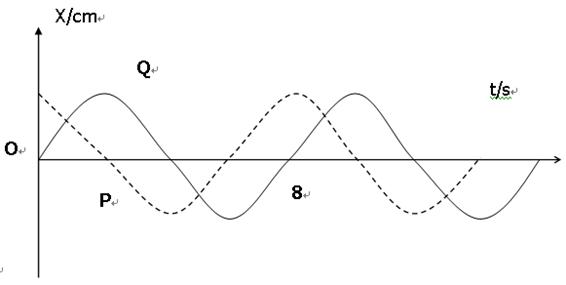
在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S,从S出的光线SA以角度θ入射到玻璃板上表面,经过玻璃板后从下表面射出,如图所示,若此光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等,点光源S到玻璃板上表面的垂直距离l是多少?
如图所示,倾角θ=37°的斜面底端光滑的水平面BC平滑连接着半径r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块,从距地面h=2.7m处沿斜面由静止开始下滑,小物块与斜面间的动摩擦因数μ=0.25,求:(sin37°=0.6,cos37°=0.8,g=10m/s2)
(1)物块滑到斜面底端B时的速度大小。
(2)物块沿圆轨道运动到最高点A后在空中做平抛运动落在水平面BC上,已知平抛
运动水平位移为1.8m,求物体运动至A点时对圆轨道的压力大小。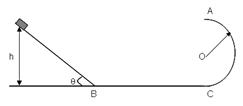
2007年10月24日,“嫦娥一号”卫星星箭分离,卫星进入绕地球轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④。11月5日11时,当卫星经过距月球表面高度为h的A点时,再一次实施变轨,进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T的月球极月圆轨道⑦。如图所示,已知月球半径为R。
(1)请回答:“嫦娥一号”在完成第三次近地变轨时需要加速还是减速?
(2)写出月球表面重力加速度的表达式。