(本小题满分12分)已知函数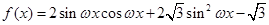 (
( )的最小正周期为
)的最小正周期为 .
.
(Ⅰ)求函数 的单调增区间;
的单调增区间;
(Ⅱ)将函数 的图象向左平移
的图象向左平移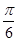 个单位,再向上平移
个单位,再向上平移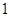 个单位,得到函数
个单位,得到函数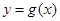 的图象.求
的图象.求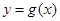 在区间
在区间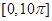 上零点的个数.
上零点的个数.
已知直线l1:x-2y-1=0,直线l2:ax-by+1=0,其中a,b∈{1,2,3,4,5,6}.
(1) 求直线l1与l2相交的概率;
(2) 求直线l1与l2的交点位于第一象限的概率.
某小组共有A、B、C、D、E五位同学,他们的身高(单位:m)以及体重指标(单位:kg/m2)如下表所示:
| A |
B |
C |
D |
E |
|
| 身高 |
1.69 |
1.73 |
1.75 |
1.79 |
1.82 |
| 体重指标 |
19.2 |
25.1 |
18.5 |
23.3 |
20.9 |
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
判断下列命题正确与否.
(1)先后掷两枚质地均匀的硬币,等可能出现“两个正面”“两个反面”“一正一反”三种结果;
(2)某袋中装有大小均匀的三个红球、两个黑球、一个白球,任取一球,那么每种颜色的球被摸到的可能性相同;
(3)从-4,-3,-2,-1,0,1,2中任取一数,取到的数小于0与不小于0的可能性相同;
(4)分别从3名男同学、4名女同学中各选一名代表,男、女同学当选的可能性相同.
从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) |
[80,85) |
[85,90) |
[90,95) |
[95,100) |
| 频数(个) |
5 |
10 |
20 |
15 |
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有一个的概率.
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 质量指标(x,y,z) |
(1,1,2) |
(2,1,1) |
(2,2,2) |
(1,1,1) |
(1,2,1) |
| 产品编号 |
A6 |
A7 |
A8 |
A9 |
A10 |
| 质量指标(x,y,z) |
(1,2,2) |
(2,1,1) |
(2,2,1) |
(1,1,1) |
(2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取两件产品,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.