（本小题满分10分）
某批次的某种灯泡共200个，对其寿命进行追踪调查，将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级，其中寿命大于或等于500天的灯泡是优等品，寿命小于300天的灯泡是次品，其余的灯泡是正品.
| 寿命（天） |
频数 |
频率 |
 |
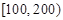10 |
 |
 |
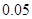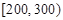30 |
 |
 |
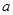70 |
 |
 |
 |
 |
 |
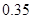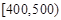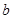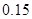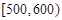60 |
 |
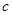| 合计 |
200 |
 |
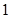（Ⅰ）根据频率分布表中的数据，写出a，b，c的值；
（Ⅱ）某人从这200个灯泡中随机地购买了1个，求此灯泡恰好不是次品的概率；
，
，
均为锐角.
；（2）求
.
上的动点，O是原点，N是射线OM上的点，若
，求点N的轨迹方程。
的准线与
轴交点为
，过点
交抛物线与不同的点
两点.
中点的轨迹方程；
，求证：
.