小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围;
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
如图,已知CD∥AB,OE平分∠BOD,OE⊥OF,∠CDO=62°,求∠DOF的度数.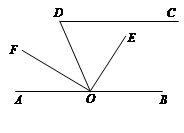
解下列方程组.(每小题5分,共30分)
(1) 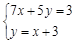 (2)
(2) 
(3) 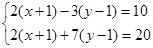 (4)
(4) 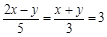
(5) 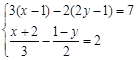 (6)
(6) 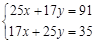
如图,矩形ABCD中,AB=3,BC=4,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积, 表示矩形NFQC的面积
表示矩形NFQC的面积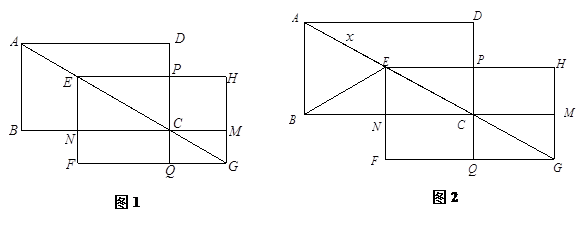
(1)S与 吗?请说明理由.
吗?请说明理由.
(2)设AE=x,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最大值是多少?
(3)如图2,连结BE,当AE为何值时, 是等腰三角形.
是等腰三角形.
工业园区某消毒液工厂,今年四月份以前,每天的产量与销售量均为400箱.进入四月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量 (箱)与生产时间
(箱)与生产时间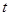 (月份)之间的函数图象.
(月份)之间的函数图象.
(1)四月份的平均日销售量为多少箱?
(2)为满足市场需求,该厂打算在投资不超过138万元的情况下,购买5台新设备,准备在新设备和原设备的共同工作下扩大生产规模,使日产量不低于四月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
| 型号 |
A |
B |
| 价格(万元/台) |
28 |
25 |
| 日产量(箱/台) |
50 |
40 |
请问:有哪几种购买设备的方案?若为了使日产量最大,应选择哪种方案?
如图,已知二次函数y=ax2-4x+c的图像经过点A和点B.(1)求该二次函数的表达式;
(2)点E(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求Q到y轴的距离.
(3)设抛物线与y轴的的交点为C,点P为抛物线的对称轴上的一动点,求使∠PCB=90°的点P的坐标.