如图，在平面直角坐标系xOy中，二次函数y=﹣x2+bx+c的图象与x轴相交于点A（4，0），与y轴相交于点B（0，4），动点C是从点A出发，向O点运动，到达0点时停止运动，过点C作EC⊥x轴，交直线AB于点D，交抛物线于点E．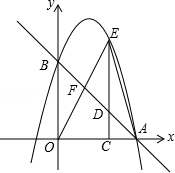
（1）求二次函数的解析式；
（2）连接OE交AB于F点，连接AE，在动点C的运动过程中，若△AOF的面积是△AEF面积的2倍，求点C的坐标？
（3）在动点C的运动过程中，△DEF能否为等腰三角形？若能，请直接写出点F的坐标；若不能，请说明理由．
在结束了380课时初中阶段数学内容的教学后，唐老师计划安排60课时用于总复习，根据数学内容所占课时比例，绘制如下统计图表（图1～图3），请根据图表提供的信息，回答下列问题：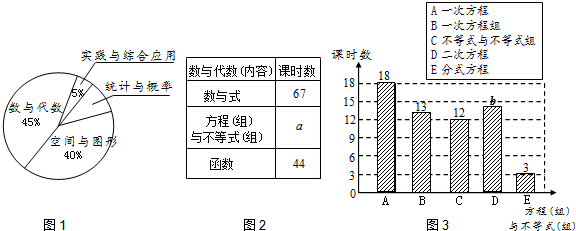
（1）图1中"统计与概率"所在扇形的圆心角为度；
（2）图2、3中的
，
；
（3）在60课时的总复习中，唐老师应安排多少课时复习"图形与几何"内容？
如图，在△ABC中，D．E分别是AB、AC边的中点．求证：DE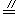
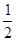BC．
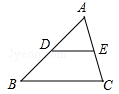
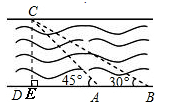
如图所示，我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度．小宇同学在A处观测对岸C点，测得∠CAD＝45°，小英同学在距A处50米远的B处测得∠CBD＝30°，请你根据这些数据算出河宽．（精确到0.01米，参考数据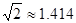
，
）
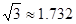在□ABCD中，∠BCD的平分线与BA的延长线相交于点E，BH⊥EC于点H，求证：CH＝EH．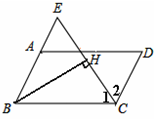
解不等式：
，并把解集在数轴上表示出来．