某地上年度电价为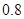 元,年用电量为
元,年用电量为 亿千瓦时.本年度计划将电价调至
亿千瓦时.本年度计划将电价调至 之间,经测算,若电价调至
之间,经测算,若电价调至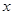 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与
(亿千瓦时)与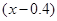 元成反比例.又当
元成反比例.又当 时,
时, .
.
(1)求 与
与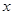 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为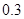 元,则电价调至多少时,本年度电力部门的收益将比上年增加
元,则电价调至多少时,本年度电力部门的收益将比上年增加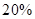 ?[收益=用电量×(实际电价-成本价)]
?[收益=用电量×(实际电价-成本价)]
已知抛物线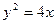 的焦点是F,点P是抛物线上的动点,又有点A(3,2),求
的焦点是F,点P是抛物线上的动点,又有点A(3,2),求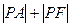 最小值,并求此时P点的坐标.
最小值,并求此时P点的坐标.
如图,△ACD是等边三角形,△ABC是等腰直角
三角形,∠ACB=90°,BD交AC于E,AB=2.
(1)求cos∠CBE的值;
(2)求AE。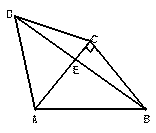
求
.本小题满分14分)
已知定义在实数集R上的偶函数 的最小值为3,且当
的最小值为3,且当 时,
时,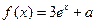 ,其中e是自然对数的底数
,其中e是自然对数的底数 。
。
(1)求函数 的解析式;
的解析式;
(2)若实数 使得存在
使得存在 ,只要
,只要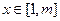 ,就有
,就有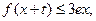 求正整
求正整
数n的最大值。
.已知定圆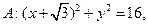 圆心为A;动圆M过点
圆心为A;动圆M过点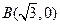 且与圆A相切,圆心M 的坐标为
且与圆A相切,圆心M 的坐标为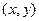 且
且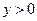 ,它的轨迹记为
,它的轨迹记为 C。
C。
(1)求曲线 C的方程;
C的方程;
(2)过一点N(1,0)作两条互相垂直的直线与曲线C分别交于点P和Q,试问这两条直线能否使得向量 互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。
互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。