(本小题满分12分)一种药在病人血液中的含量不低于2克时,它才能起到有效治疗的作用.已知每服用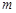 (
(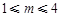 且
且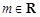 )个单位的药剂,药剂在血液中的含量
)个单位的药剂,药剂在血液中的含量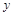 (克)随着时间
(克)随着时间 (小时)变化的函数关系式近似为
(小时)变化的函数关系式近似为 ,其中
,其中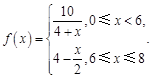
(Ⅰ)若病人一次服用3个单位的药剂,则有效治疗时间可达多少小时?
(Ⅱ)若病人第一次服用2个单位的药剂,6个小时后再服用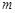 个单位的药剂,要使接下来的2小时中能够持续有效治疗,试求
个单位的药剂,要使接下来的2小时中能够持续有效治疗,试求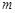 的最小值.
的最小值.
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在"25周岁以上(含25周岁)"和"25周岁以下"分为两组,再将两组工人的日平均生产件数分为5组: , , , , ,分别加以统计,得到如图所示的频率分布直方图.
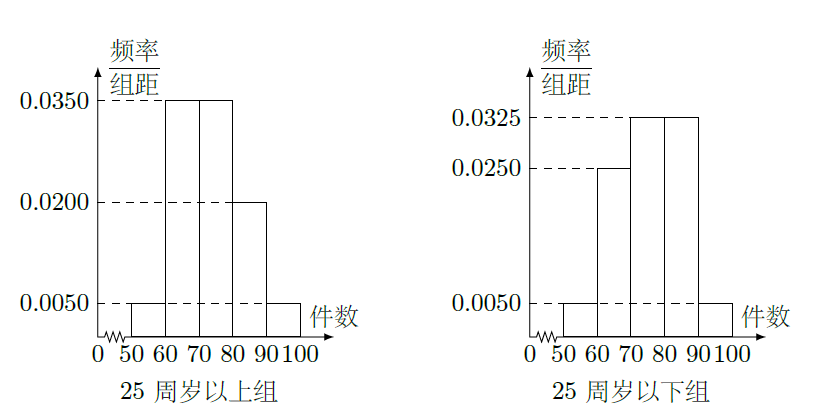
(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名"25周岁以下组"工人的概率;
(II)规定日平均生产件数不少于80件者为"生产能手",请你根据已知条件完成列联表,并判断是否有90%的把握认为"生产能手与工人所在的年龄组有关"?
附: (注:此公式也可以写成 )
| 0.100 |
0.050 |
0.010 |
0.001 |
|
| 2.706 |
3.841 |
6.635 |
10.828 |
如图,在四棱柱 中, 平面 , , .
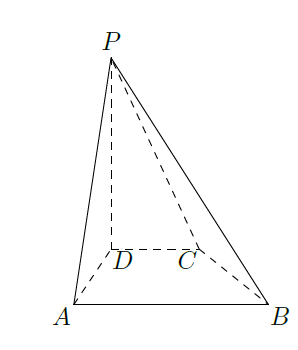
(1)当正视方向与向量
的方向相同时,画出四棱锥
的正视图(要求标出尺寸,并写出演算过程);
(2)若
为
的中点,求证:求二面角
.
(3)求三棱锥 的体积.
已知等差数列
的公差
,前
项和为
.
(I)若
成等比数列,求
;
(II)若
,求
的取值范围.
如图, D是直角△ABC斜边BC上一点,AB=AD,记∠CAD= ,∠ABC=
,∠ABC= .
.
(1)证明  ;
;
(2)若AC=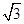 DC,求
DC,求 的值.
的值.
已知数列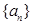 是等差数列,且
是等差数列,且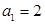 ,
,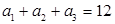 .
.
⑴ 求数列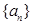 的通项公式;
的通项公式;
⑵ 令
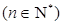 ,求数列
,求数列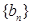 的前
的前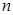 项和.
项和.