(本小题满分13分)若存在实常数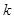 和
和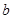 ,使得函数
,使得函数 和
和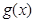 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: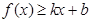 和
和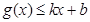 ,则称直线
,则称直线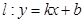 为
为 和
和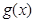 的“隔离直线”.已知
的“隔离直线”.已知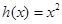 ,
,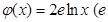 为自然对数的底数).
为自然对数的底数).
(1)求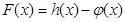 的极值;
的极值;
(2)函数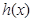 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
已知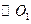 的极坐标方程为
的极坐标方程为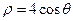 .点
.点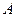 的极坐标是
的极坐标是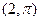 .
.
(Ⅰ)把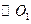 的极坐标方程化为直角坐标参数方程,把点
的极坐标方程化为直角坐标参数方程,把点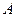 的极坐标化为直角坐标.
的极坐标化为直角坐标.
(Ⅱ)点M(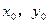 )在
)在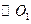 上运动,点
上运动,点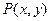 是线段
是线段 的中点,求点
的中点,求点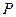 运动轨迹的直角坐标方程.
运动轨迹的直角坐标方程.
某养殖厂需定期购买饲料,每公斤饲料的价格为1.8元,一次购买饲料所需的运费是300元.已知该厂的饲料日平均保管费用为每公斤每天0.03元,且每天清晨需从仓库搬出饲料200公斤喂食家禽,规定购买饲料的当天不计新进货物的保管费用.例如:若每三天进货一次,则每次进货量是600公斤,该批饲料的保管费用共为200×0.03+400×0.03=18(元).
(Ⅰ)求该厂多少天购买一次饲料才能使平均每天支付的总费用最小;
(Ⅱ)若提供饲料的公司规定,当一次购买饲料不少5吨时其价格可享受八五折优惠(即原价的85%).问该厂是否考虑利用此优惠条件,请说明理由.
数列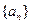 的前
的前 项和为
项和为 ,且
,且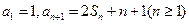 。
。 (1)求数列
(1)求数列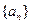 的通项公式;
的通项公式; (2)设等差数列
(2)设等差数列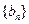 各项均为正数,满足
各项均为正数,满足 ,且
,且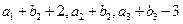 ,成等比数列。证明:
,成等比数列。证明: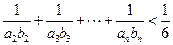 。
。
已知动圆过定点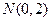 ,且与定直线
,且与定直线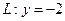 相切.
相切.
(1)求动圆圆心的轨迹C的方程;
(2)若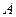 、
、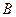 是轨迹C上的两不同动点,且
是轨迹C上的两不同动点,且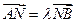 . 分别以
. 分别以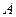 、
、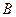 为切点作轨迹C的切线,设其交点Q,证明
为切点作轨迹C的切线,设其交点Q,证明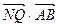 为定值.
为定值.
数列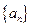 中
中 ,
,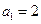 ,
, (
(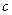 是不为零的常数,
是不为零的常数,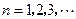 ),且
),且 成等比数列.
成等比数列.
(1)求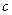 的值;
的值;
(2)求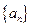 的通项公式;
的通项公式;
(3)求数列 的前
的前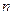 项之和
项之和