(本小题满分12分)已知四棱锥 中,底面ABCD为直角梯形,BC//AD,
中,底面ABCD为直角梯形,BC//AD, ,且PA=AB=BC=1,AD=2,
,且PA=AB=BC=1,AD=2, 平面ABCD,E为AB的中点.
平面ABCD,E为AB的中点.
(Ⅰ)证明: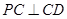 ;
;
(Ⅱ)在线段PA上是否存在一点F,使EF//平面PCD,若存在,求 的值.
的值.
某校从参加某次知识竞赛的同学中,选取 名同学将其成绩(百分制,均为整数)分成
名同学将其成绩(百分制,均为整数)分成 ,
, ,
, ,
, ,
, ,
, 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
已知数列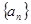 的各项均为正数,前
的各项均为正数,前 项和为
项和为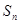 ,且
,且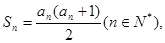
(1)求证:数列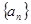 是等差数列;
是等差数列;
(2)设 求
求
选修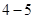 :不等式选讲.
:不等式选讲.
已知函数 的定义域为
的定义域为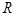 .
.
(1)求实数 的取值范围;
的取值范围;
(2)若实数 的最大值为
的最大值为 ,正数
,正数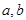 满足
满足 ,求
,求 的最小值.
的最小值.
选修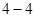 :极坐标与参数方程
:极坐标与参数方程
在直角坐标系 中,以
中,以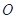 为极点,
为极点,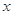 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为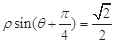 .圆
.圆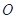 的参数方程为
的参数方程为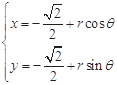 ,
,
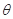 为参数,
为参数,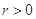
 .
.
(1)求圆心的一个极坐标;
(2)当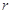 为何值时,圆
为何值时,圆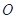 上的点到直线
上的点到直线 的最大距离为
的最大距离为 .
.
选修 :几何证明选讲
:几何证明选讲
如图,点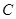 是⊙
是⊙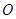 直径
直径 的延长线上一点,
的延长线上一点, 是⊙
是⊙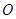 的切线,
的切线, 为切点,
为切点, 的平分线
的平分线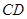 与
与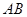 相交于点
相交于点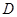 与
与 相交于点
相交于点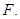
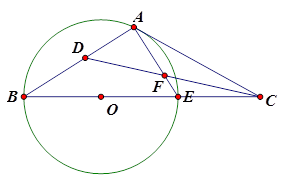
(1)求 的值;
的值;
(2)若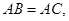 求
求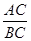 的值.
的值.