选修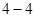
：极坐标与参数方程
在直角坐标系
中，以
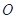为极点，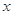
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为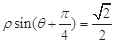
．圆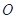的参数方程为
，
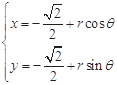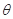为参数，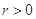
．
（1）求圆心的一个极坐标；
（2）当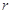
为何值时，圆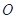上的点到直线的最大距离为
．
已知圆C经过P（4，– 2），Q（– 1，3）两点，且在y轴上截得的线段长为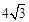
，半径小于5．
（1）求直线PQ与圆C的方程．
（2）若直线l∥PQ，且l与圆C交于点A、B，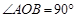
，求直线l的方程．
．已知直线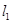
：
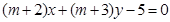和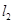
：
。
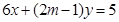问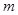
为何值时，有：（1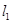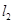）∥？（2）⊥？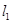
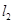如图是总体的一样本频率分布直方图，且在[15，18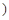
内的频数为8，求（1）样本容量；（2）若在[12,15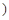内小矩形面积为
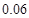，求在[12,15内的频数；（3）在（2）的条件下，求样本数据在[18,33内的频率并估计总体数据在[18,33内的频率．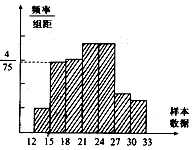
如图，在△BCD中，∠BCD＝90°，BC＝CD＝1，AB⊥平面BCD，∠ADB＝60°，E、F分别是AC、AD上的动点，且＝＝λ(0<λ<1)．
(1)判断EF与平面ABC的位置关系并给予证明；
(2)是否存在λ，使得平面BEF⊥平面ACD，如果存在，求出λ的值，如果不存在，说明理由．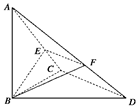
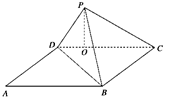
如图，矩形ABCD中，AB＝6，BC＝2，沿对角线BD将△ABD向上折起，使点A移至点P，且点P在平面BCD内的投影O在CD上．
(1) 求二面角P－DB－C的正弦值；
(2) 求点C到平面PBD的距离．