如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(1)求证:平面BCE⊥平面CDE;
(2)求二面角B-EF-D的余弦值.
若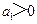 ,且
,且 ,
,
(1)令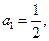 写出
写出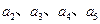 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式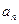 ;
;
(2)求证: 。
。
已知 ,设命题
,设命题 :函数
:函数 在
在 上单调递增,命题
上单调递增,命题 :不等式
:不等式 ,对
,对 恒成立,若
恒成立,若 且
且 为假,
为假, 或
或 为真,求
为真,求 的取值范围
的取值范围
已知椭圆 ,且C1,C2的公共弦AB过椭圆C1的右焦点。
,且C1,C2的公共弦AB过椭圆C1的右焦点。
(1)求椭圆的焦点坐标及m=0,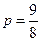 时
时 的焦点坐标;
的焦点坐标;
(2)当AB⊥x轴时,判断抛物线C2的焦点是否在直线AB上;
(3)是否存在m,p的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的m,p的值;若不存在,请说明理由。
如图,在三棱柱 中,
中,  ,
, ,
, ,点D是
,点D是 上一点,且
上一点,且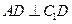 。
。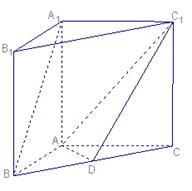
(1)求证:平面 平面
平面 ;
;
(2)求证: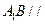 平面
平面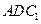 ;
;
(3)求二面角 的余弦值
的余弦值
湖南大学自主招生选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手被淘汰的概率;
(2)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望