如图, 已知网格上小正方形的边长为1。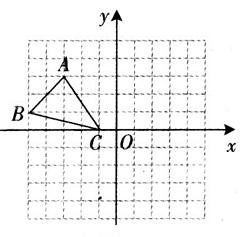
(1)分别写出点A,B,C的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法);
某 市为争创全国文明卫生城,2008年市政府对市区绿化工程投
市为争创全国文明卫生城,2008年市政府对市区绿化工程投
入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间
每年投入资金的年平均增长率相同.
(1)求该市对市区绿化工程投入资金的年平均增长率;
(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?
本题满分8分)“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:
(1)这次抽查的家长总人数为;
(2)请补全条形统计图和扇形统计图;
(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率
是.
 |
本题满分8分)求证:角平分线上的点到这个角的两边距离相等.
已知:
求证:
证明:
 |
解二元一次方程组:
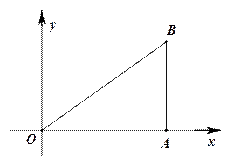
如图,已知O(0,0)、A(4,0)、B(4,3).动点P从O点出发,以每秒3个单位的速度,沿△OAB的边0A、AB、B0作匀速运动;动直线l从AB位置出发,以每秒1个单位的速度向x轴负方向作匀速平移运动.若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动.
(1)当P在线段OA上运动时,求直线l与以P为圆心、1为半径的圆相交时t的取值范围;
(2)当P在线段AB上运动时,设直线l分到与OA、OB交于C、D,试问:四边形CPBD是否可能为菱形?若能,求出此时t的值;若不能,请说明理由,并说明如何改变直线l的出发时间,使得四边形CPBD会是菱形.