如图，已知O(0，0)、A(4，0)、B(4，3)．动点P从O点出发，以每秒3个单位的速度，沿△OAB的边0A、AB、B0作匀速运动；动直线l从AB位置出发，以每秒1个单位的速度向x轴负方向作匀速平移运动．若它们同时出发，运动的时间为t秒，当点P运动到O时，它们都停止运动．
(1)当P在线段OA上运动时，求直线l与以P为圆心、1为半径的圆相交时t的取值范围；
(2)当P在线段AB上运动时，设直线l分到与OA、OB交于C、D，试问：四边形CPBD是否可能为菱形?若能，求出此时t的值；若不能，请说明理由，并说明如何改变直线l的出发时间，使得四边形CPBD会是菱形．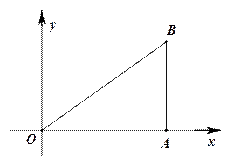
如图，在直角坐标系中，以点A（
，0 ）为圆心，以2为半径的圆与x轴相交于点B、C，与y轴相交于点D、E
（1）若抛物线
经过C、D两点，求抛物线的表达式，并判断点B是否在该抛物线上
（2）在（1）中的抛物线的对称轴上求一点P，使得△PBD的周长最小
（3）设Q为（1）中的抛物线对称轴上的一点，在抛物线上是否存在这样的点M，使得四边形BCQM是平行四边形，若存在，求出点M的坐标；若不存在，说明理由
张经理到老王的果园里一次性采购一种水果,他俩商定：张经理的采购价
元/吨与采购量
吨之间函数关系的图象如图中的折线段
所示（不包含端点
,但包含端点
）.
（1）求与之间的函数关系式；
（2）已知老王种植水果的成本是2800元/吨，那么张经理的采购量为多少时，老王在这次买卖中所获的利润
最大？最大利润是多少？
如图，已知A、B、C、D四点均在以BC为直径的⊙O上，AD∥BC，AC平分∠BCD，∠ADC=120°，BC=4．
（1）求扇形ODC的面积；
（2）求四边形ABCD的周长.
如图所示,OA、OB、OC都是圆O的半径,∠AOB=2∠BOC．求证:∠ACB=2∠BAC.
请你依据右面图框中的寻宝游戏规则，探究“寻宝游戏”的奥秘：
（1）用树状图表示出所有可能的寻宝情况；
（2）求在寻宝游戏中胜出的概率。