甲乙两超市分别用3000元以相同的进价购进质量相同的苹果。甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%的价格销售。乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按照甲超市大、小两种苹果售价的平均数定价。若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计)问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较那种销售方式更合算。
如图,反比例函数
的图象与直线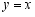 交于点
交于点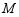 ,
,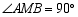 ,其两边分别与两坐标轴的正半轴交于点
,其两边分别与两坐标轴的正半轴交于点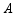 ,
,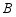 ,四边形
,四边形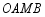 的面积为6.
的面积为6.
(1)求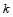 的值;
的值;
(2)点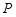 在反比例函数
的图象上,若点
在反比例函数
的图象上,若点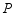 的横坐标为3,
的横坐标为3,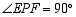 ,其两边分别与
,其两边分别与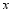 轴的正半轴,直线
轴的正半轴,直线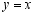 交于点
交于点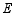 ,
,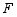 ,问是否存在点
,问是否存在点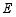 ,使得
,使得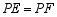 ?若存在,求出点
?若存在,求出点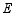 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
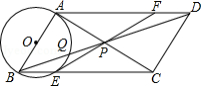
如图,在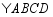 中,
中,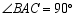 ,对角线
,对角线 ,
, 相交于点
相交于点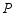 ,以
,以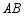 为直径的
为直径的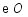 分别交
分别交 ,
, 于点
于点 ,
, ,连接
,连接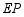 并延长交
并延长交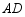 于点
于点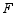 .
.
(1)求证: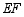 是
是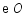 的切线;
的切线;
(2)求证: .
.
甲车从 地驶往
地驶往 地,同时乙车从
地,同时乙车从 地驶往
地驶往 地,两车相向而行,匀速行驶,甲车距
地,两车相向而行,匀速行驶,甲车距 地的距离
地的距离 与行驶时间
与行驶时间 之间的函数关系如图所示,乙车的速度是
之间的函数关系如图所示,乙车的速度是
(1)求甲车的速度;
(2)当甲乙两车相遇后,乙车速度变为 ,并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求
,并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求 的值.
的值.

在一次数学文化课题活动中,把一副数学文化创意扑克牌中的4张扑克牌(如图所示)洗匀后正面向下放在桌面上,从中随机抽取2张牌,请你用列表或画树状图的方法,求抽取的2张牌的数字之和为偶数的概率.

小梅家的阳台上放置了一个晒衣架如图1,图2是晒衣架的侧面示意图, ,
, 两点立于地面,将晒衣架稳固张开,测得张角
两点立于地面,将晒衣架稳固张开,测得张角 ,立杆
,立杆 ,小梅的连衣裙穿在衣架后的总长度为
,小梅的连衣裙穿在衣架后的总长度为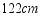 ,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:
,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据: ,
, ,
,
