数学课上,李老师出示了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F. (请你接着完成以下解答过程)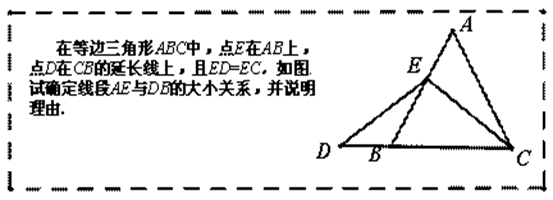
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=1,则CD的长为 (请你直接写出结果).
公司经营甲、乙两种商品,每件甲种商品进价12万元,售价14.5万元;每件乙种商品进价8万元,售价lO万元,且它们的进价和售价始终不变.现准备购进甲、乙两种商品共20件,所用资金不低于190万元,不高于200万元.该公司有哪几种进货方案?
该公司采用哪种进货方案可获得最大利润?最大利润是多少?
直线y=k1x+b与双曲线y=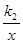 只有—个交点A(1,2),且与x轴、y轴分别交于B,C 两点,AD垂直平分OB,垂足为D,求直线、双曲线的解析式.
只有—个交点A(1,2),且与x轴、y轴分别交于B,C 两点,AD垂直平分OB,垂足为D,求直线、双曲线的解析式.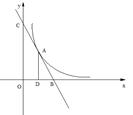
甲乙两人加工同一种玩具,甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等,已知甲乙两人每天共加工35个玩具,求甲乙两人每天各加工多少个玩具?
解方程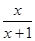 -
- =1
=1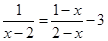
化简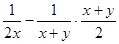
(1+
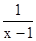 )÷
)÷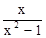 .
.