教室内有5个学生,分别佩戴1号到5号的校徽,任选3人记录他们的校徽号码。
(1)求最小号码为2的概率;
(2)求三个号码中至多有一个偶数的概率。
已知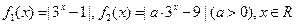 ,
,
且 .
.
(Ⅰ)当 时,求
时,求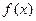 在
在 处的切线方程;
处的切线方程; (Ⅱ)当
(Ⅱ)当 时,设
时,设 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为 (闭区间
(闭区间 的长度定义为
的长度定义为 ),试求
),试求 的最大值;
的最大值;
已知等差数列 的前
的前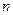 项和为
项和为 ,公差
,公差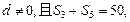
 成等比数列.
成等比数列.
(Ⅰ)求数列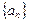 的通项公式;
的通项公式;
(Ⅱ)若从数列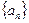 中依次取出第2项、第4项、第8项,……,
中依次取出第2项、第4项、第8项,……, ,……,按原来顺序组成一个新数列
,……,按原来顺序组成一个新数列 ,记该数列的前
,记该数列的前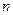 项和为
项和为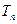 ,求
,求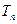 的表达式.
的表达式.
已知二次函数 (
( 为常数且
为常数且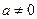 )满足条件
)满足条件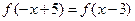 ,且方程
,且方程 有等根.
有等根.
(1)求 的解析式;
的解析式;
(2)是否存在实数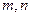 使
使 的定义域和值域分别为
的定义域和值域分别为 和
和 ?如果存在,求出
?如果存在,求出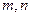 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
已知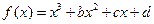 的图象过点
的图象过点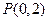 ,且在点
,且在点 处的切线方程为
处的切线方程为 .(1)求
.(1)求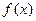 的解析式;(2)求函数
的解析式;(2)求函数 的单调区间.
的单调区间.
给出函数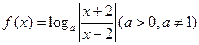 ,(1) 求函数定义域;(2)判断函数的奇偶性;(3)求使y=
,(1) 求函数定义域;(2)判断函数的奇偶性;(3)求使y=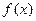 图象在
图象在 轴上方的
轴上方的 取值范围.
取值范围.