如图,正方形ABCD的边长为2,E是BC的中点,以点A为中心,把△ABE逆时针旋转90°,设点E的对应点为F.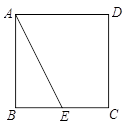
(1)画出旋转后的三角形.
(2)在(1)的条件下,
①求EF的长;
②求点E经过的路径弧EF的长.
(成都)(本小题满分10分)已知AC,EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90.
(1)如图①,当四边形ABCD和EFCG均为正方形时,连接BF.
i)求证:△CAE∽△CBF;
ii)若BE=1,AE=2,求CE的长;
(2)如图②,当四边形ABCD和EFCG均为矩形,且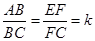 时,若BE=1,AE=2,CE=3,求k的值;
时,若BE=1,AE=2,CE=3,求k的值;
(3)如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)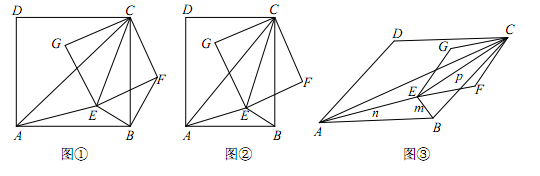
(成都)(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线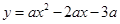 (
(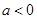 )与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:
)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l: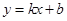 与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为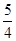 ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.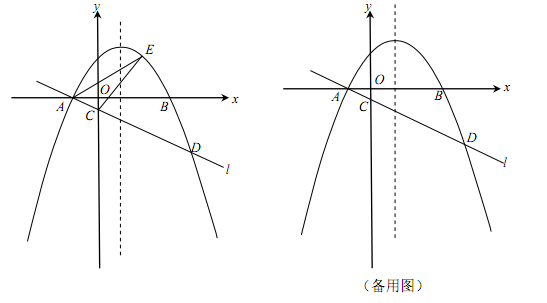
(乐山)“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表: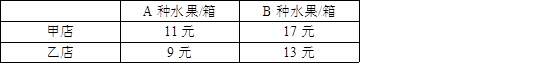
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
(攀枝花)某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价﹣进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.