（本小题满分10分）选修4—4：坐标系与参数方程
已知曲线
的参数方程为
（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
．
（1）把的参数方程化为极坐标方程；
（2）求与交点的极坐标
．
已知函数f(x)＝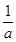
－
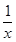(a＞0，x＞0)．
(1)用函数的单调性定义证明：f(x)在(0，＋∞)上是增函数；
(2)若f(x)在[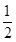
，2]上的值域是[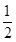，2]，求实数a的值．
已知奇函数f(x)在定义域[－2,2]内单调递减，求满足f(1－m)＋f(1－m2)<0的实数m的取值范围．
已知函数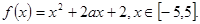
（1）
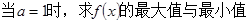
（2）
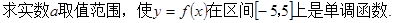
(1) 已知集合
，若
，求实数
的值
(2)已知集合A={x|x2-5x-6=0},集合B={x|mx+1=0}若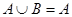
，求实数m组成的集合.
已知函数f(x)是定义在（0，+∞）上的单调增函数，满足f(xy)=f(x)+f(y),f(3)=1
（1）求f(1)的值
（2）若满足f(x) +f(x-8)≤2 求x的取值范围