已知:y=y1+y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=-1时,y=1.求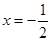 时,y的值.
时,y的值.
如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.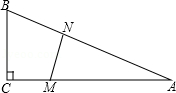
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是弧AC的中点,⊙O的半径为1,求图中阴影部分的面积.
如图,在直角坐标系xOy中,直线 与双曲线
与双曲线 相交于
相交于 、B
、B 两点,矩形
两点,矩形 的边
的边 恰好被点
恰好被点 平分,边
平分,边 交双曲线于
交双曲线于 点,四边形
点,四边形 的面积为2.
的面积为2.
(1)求n的值;
(2)求不等式 的解集
的解集
如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1: ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
一个不透明的袋子里装有编号分别为1、2、3的球(除编号以为,其余都相同),其中1号球1个,3号球3个,从中随机摸出一个球是2号球的概率为 .
.
(1)求袋子里2号球的个数.
(2)甲、乙两人分别从袋中摸出一个球(不放回),甲摸出球的编号记为x,乙摸出球的编号记为y,用列表法求点A(x,y)在直线y=x下方的概率.