在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”.例如点(-1,-1),(0,0),( ,
, ),……都是“梦之点”,显然,这样的“梦之点”有无数个.
),……都是“梦之点”,显然,这样的“梦之点”有无数个.
(1)若点P(2,m)是反比例函数 (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,y1),B(x2,y2),且满足-2<x1<2,|x1-x2|=2,令 ,试求t的取值范围.
,试求t的取值范围.
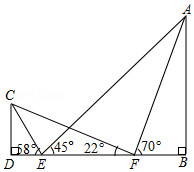
如图,为了测量建筑物 的高度,在 处竖立标杆 ,标杆的高是 ,在 上选取观测点 、 ,从 测得标杆和建筑物的顶部 、 的仰角分别为 、 .从 测得 、 的仰角分别为 、 .求建筑物 的高度(精确到 .(参考数据: , , .
甲口袋中有2个白球、1个红球,乙口袋中有1个白球、1个红球,这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球.
(1)求摸出的2个球都是白球的概率.
(2)下列事件中,概率最大的是 .
.摸出的2个球颜色相同 .摸出的2个球颜色不相同
.摸出的2个球中至少有1个红球 .摸出的2个球中至少有1个白球
随机抽取某理发店一周的营业额如下表(单位:元)
|
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
星期日 |
合计 |
|
540 |
680 |
760 |
640 |
960 |
2200 |
1780 |
7560 |
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
如图,在四边形 中, , . 是四边形 内一点,且 .求证:
(1) ;
(2)四边形 是菱形.

刘阿姨到超市购买大米,第一次按原价购买,用了105元,几天后,遇上这种大米8折出售,她用140元又买了一些,两次一共购买了 .这种大米的原价是多少?