某班组织知识竞赛,已知题目共有10道,随机抽取3道让某人回答,规定至少要答对其中2道才能通过初试,他只能答对其中6道,试求:
(1)抽到他能答对题目数的分布列;
(2)他能通过初试的概率.
已知函数
(I)若 ,求sin2x的值;
,求sin2x的值;
(II)求函数 的最大值与单调递增区间.
的最大值与单调递增区间.
已知等差数列 的公差
的公差 ,它的前n项和为
,它的前n项和为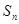 ,若
,若 且
且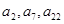 成等比数列.
成等比数列.
(I)求数列 的通项公式;
的通项公式;
(II)设数列 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.
(本小题满分12分)设函数 的图象上两点P1(x1,y1)、P2(x2,y2),若
的图象上两点P1(x1,y1)、P2(x2,y2),若 ,且点P的横坐标为
,且点P的横坐标为 .
.
(1),求证:P点的纵坐标为定值,并求出这个定值;
(2),求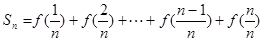
(3),记Tn为数列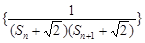 的前n项和,若
的前n项和,若 对一切n∈N*都成立,试求a的取值范围。
对一切n∈N*都成立,试求a的取值范围。
(本小题满分10分)求过点P(2,2)且与曲线y=x2相切的直线方程.
已知数列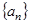 的前
的前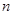 项和
项和 满足
满足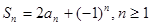 .
.
(1)写出数列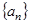 的前三项
的前三项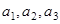 ;
;
(2)求数列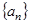 的通项公式;
的通项公式;
(3)证明:对任意的整数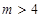 ,有
,有 .
.