在长方体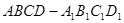 中,
中, ,过
,过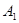 ,
, ,
,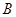 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体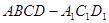 ,这个几何体的体积为
,这个几何体的体积为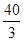 .
.
(1)证明:直线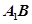 ∥平面
∥平面 ;
;
(2)求棱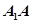 的长;
的长;
(3)在线段 上是否存在点
上是否存在点 ,使直线
,使直线 与
与 垂直,如果存在,求线段
垂直,如果存在,求线段 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
如图,四边形 中(图1),
中(图1),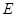 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为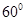 (如图2)
(如图2)
(1)求证: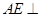 平面
平面 ;
;
(2)求二面角A—DC—B的余弦值。
已知函数f(x)=ln x-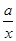 .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为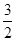 ,求a的值;
,求a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求a的取值范围.
为迎接我校110周年校庆,校友会于日前举办了一次募捐爱心演出,有1000 人参加,每人一张门票,每张100元. 在演出过程中穿插抽奖活动.第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动.第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数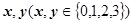 ,满足
,满足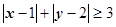 电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
(1)已知校友甲在第一轮抽奖中被抽中,求校友甲在第二轮抽奖中获奖的概率;
(2)若校友乙参加了此次活动,求校友乙参加此次活动收益的期望;
已知向量m=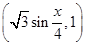 ,n=
,n= .
.
(1)若m·n=1,求cos 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
(12分)已知函数f(x)= (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.