用一与底面成30°角的平面去截一圆柱,已知圆柱的底面半径为4,求截面椭圆的方程.
盒中有6只灯泡,其中有2只是次品,4只是正品.从中任取2只,试求下列事件的概率.
(Ⅰ)取到的2只都是次品;
(Ⅱ)取到的2只中恰有一只次品.
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中 120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.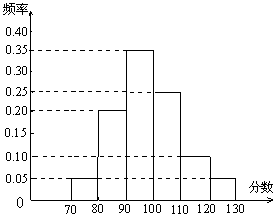
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线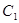 的极坐标方程是
的极坐标方程是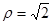 ,曲线
,曲线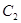 的参数方程是
的参数方程是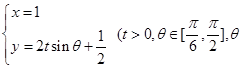 是参数).
是参数).
(1)写出曲线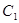 的直角坐标方程和曲线
的直角坐标方程和曲线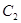 的普通方程;
的普通方程;
(2)求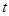 的取值范围,使得
的取值范围,使得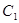 ,
,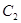 没有公共点.
没有公共点.
(本小题满分10分)选修4-5:不等式选讲
已知函数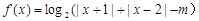 .
.
(1)当 时,求函数
时,求函数 的定义域;
的定义域;
(2)若关于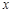 的不等式
的不等式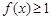 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.
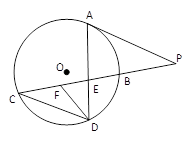
(本小题满分10分)选修4-1:几何证明选讲
如图所示,已知 与⊙
与⊙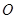 相切,
相切, 为切点,
为切点, 为割线,
为割线,
弦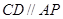 ,
, 、
、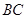 相交于
相交于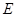 点,
点,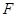 为
为 上一点,且
上一点,且 ·
· .
.
(1)求证: ;
;
(2)求证: ·
· =
=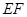 ·
· .
.