如图所示，有三个宽度均相等的区域I、Ⅱ、Ⅲ；在区域I和Ⅲ内分别为方向垂直于纸面向外和向里的匀强磁场（虚线为磁场边界面，并不表示障碍物），区域I磁感应强度大小为B，某种带正电的粒子，从孔O1以大小不同的速度沿图示与
夹角α=300的方向进入磁场（不计重力）。已知速度为v0和2v0时，粒子仅在区域I内运动且运动时间相同，均为t0。
（1）试求出粒子的比荷q/m、速度为2v0的粒子从区域I射出时的位置离O1的距离L；
（2）若速度为v的粒子在区域I内的运时间为t0/5，在图中区域Ⅱ中O1O2上方加竖直向下的匀强电场，O1O2 下方对称加竖直向上的匀强电场，场强大小相等，使速度为v的粒子每次均垂直穿过I、Ⅱ、Ⅲ区域的边界面并能回到O1点，则请求出所加电场场强大小与区域Ⅲ磁感应强度大小。
一物体做匀加速直线运动，途中由A经B到C历时4s，前2s从A到B和后2s从B到C的位移分别为24m和32m。求：
（1）物体运动的加速度为多少？
（2）物体在A点和C点的瞬时速度的分别为多少？
半径为R的水平圆台，可绕通过圆心O的竖直光滑细轴CC′转动，如图所示，圆台上沿相互垂直的两个半径方向刻有凹槽，质量为mA的物体A放在一个槽内，物体A与槽底间的动摩擦因数为μ，质量为mB的物体B放在另一个槽内，此槽是光滑的．AB间用一长为l（l<R）且不可伸长的轻绳绕过细轴相连．已知圆台做匀速转动，且A、B两物体相对圆台不动（A、B两物体可视为质点，物体的最大静摩擦力近似等于滑动摩擦力）．
（1）当圆台转动的角速度为ω0，OA的长度为l1时，试写出A、B两个物体受到的向心力大小的表达式．
（2）不论圆台转动的角速度为多大，要使物体A和槽之间恰好没有摩擦力，则OA的长为多大？
（3）设OA长为x，试分析圆台的角速度ω和物体A到圆心的距离x所应满足的条件．
山地滑雪是人们喜爱的一项体育运动．一滑雪坡由AB和BC组成，AB为斜坡，BC是半径为R =" 5" m的圆弧，圆弧与斜面相切于B点，与水平面相切于C点，如图所示．AC竖直高度差h1 =" 9.8" m，竖直台阶CD高度差为h2 =" 5" m．运动员连同滑雪装备的总质量为80 kg，从A点由静止滑下，通过C点后飞落到水平地面DE上．不计空气阻力和轨道的摩擦阻力，取g="10" m/s2．求：
⑴ 运动员到达C点的速度vc的大小；
⑵ 运动员刚到C点时轨道的对他的支持力大小；
⑶ 运动员在水平地面上落地点到D点的距离．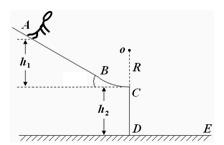
北京时间2011年2月18日晚6时，在经历了260天的密闭飞行后，中国志愿者王跃走出“火星-500”登陆舱，成功踏上模拟火星表面，在“火星”首次留下中国人的足迹．王跃拟在“火星”表面进行装置如图所示的实验，将与导轨间动摩擦因数 μ = 0.50滑块装上一个遮光板，沿水平导轨匀减速地依次通过光电门A、B．滑块通过光电门的速度分别为 v1 = 4.0m/s、v2 = 2.0m/s，从A运动到B的时间为t = 1.0s．试求：
⑴ 滑块运动时的加速度a；
⑵ 光电门A、B之间的距离s；
⑶ “火星”的重力加速度g火．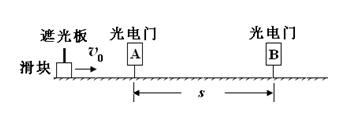
有一平行板电容器，内部为真空，两个电极板的间距为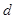
，极板的长为L，极板间有一均匀电场，U为两极板间的电压，电子从极板左端的正中央以初速
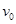射入，其方向平行于极板，并打在极板边缘的D点，如图甲所示。电子的电荷量用e表示，质量用
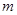表示，重力不计。回答下面各问题（用字母表示结果）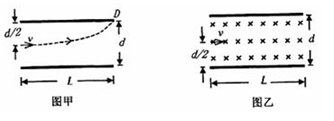
（1）求电子打到D点的动能；
（2）电子的初速V0至少必须大于何值，电子才能飞出极板？
（3）若极板间没有电场，只有垂直进入纸面的匀强磁场，其磁感应强度为B，电子从极板左端的正中央以平行于极板的初速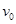射入，如图乙所示，则电子的初速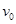为何值，电子才能飞出极板？