(本小题满分12分)已知函数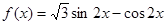
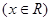 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)在锐角三角形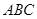 中,a、b、c分别是角A、B、C的对边,若
中,a、b、c分别是角A、B、C的对边,若 ,
,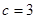 ,
,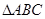 的面积为
的面积为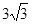 ,求
,求 的值.
的值.
在直角坐标系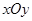 中,直线L的方程为x-y+4=0,曲线C的参数方程
中,直线L的方程为x-y+4=0,曲线C的参数方程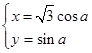
(1)求曲线C的普通方程;
(2)设点Q是曲线C上的一个动点,求它到直线L的距离的最小值.
已知直线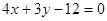 截圆心在点
截圆心在点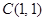 的圆
的圆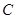 所得弦长为
所得弦长为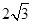 .
.
(1)求圆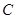 的方程;
的方程;
(2)求过点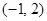 的圆
的圆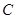 的切线方程.
的切线方程.
设函数f(x)=x3-3ax2+3bx的图像与直线12x+y-1=0相切于点(1,-11)。
(1)求a,b的值;
(2)讨论函数f(x)的单调性。
已知函数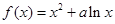 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为 .
.
(Ⅰ)求实数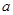 的值;
的值;
(Ⅱ)判断方程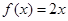 根的个数,证明你的结论;
根的个数,证明你的结论;
(Ⅲ)探究:是否存在这样的点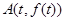 ,使得曲线
,使得曲线 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
平面内动点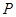 到点
到点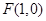 的距离等于它到直线
的距离等于它到直线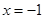 的距离,记点
的距离,记点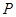 的轨迹为曲
的轨迹为曲 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)若点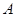 ,
,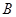 ,
,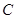 是
是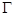 上的不同三点,且满足
上的不同三点,且满足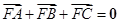 .证明:
.证明:  不可能为直角三角形.
不可能为直角三角形.