在直角坐标系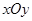 中,直线L的方程为x-y+4=0,曲线C的参数方程
中,直线L的方程为x-y+4=0,曲线C的参数方程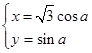
(1)求曲线C的普通方程;
(2)设点Q是曲线C上的一个动点,求它到直线L的距离的最小值.
在△ABC中,已知角A、B、C所对的三条边分别是a、b、c且满足b2=ac.
求证:0<B≤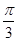 ;(2)求函数y=
;(2)求函数y=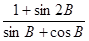 的值域.
的值域.
已知抛物线D的顶点是椭圆Q: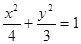 的中心O,焦点与椭圆Q的右焦点重合,点
的中心O,焦点与椭圆Q的右焦点重合,点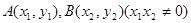 是抛物线D上的两个动点,且
是抛物线D上的两个动点,且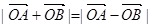
(1)求抛物线D的方程及y1y2的值;
(2)求线段AB中点轨迹E的方程;
(3)在曲线E上寻找一点,使得该点与直线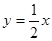 的距离最近.
的距离最近.
如图所示,在直三棱柱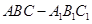 中,
中, ,
,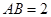 ,
,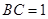 ,
, ,
, 是棱
是棱 的中点.
的中点.
(1)证明: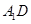
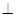 平面
平面 ;
;
(2)求二面角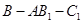 的余弦值.
的余弦值.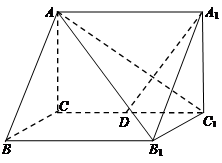
已知函数
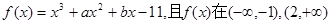 上单调递增,在(-1,2)上单调递减,又函数
上单调递增,在(-1,2)上单调递减,又函数 .
.
(1)求函数 的解析式;
的解析式;
(2)求证当
如图,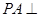 平面
平面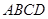 ,四边形
,四边形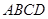 是正方形,
是正方形,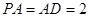 ,点
,点 、
、 、
、 分别为线段
分别为线段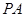 、
、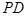 和
和 的中点. 在线段
的中点. 在线段 上是否存在一点
上是否存在一点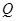 ,使得点
,使得点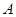 到平面
到平面 的距离恰为
的距离恰为 ?若存在,求出线段
?若存在,求出线段 的长;
的长;
若不存在,请说明理由.