(本小题满分10分)【选修4—4:坐标系与参数方程】
已知曲线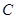 的极坐标方程为
的极坐标方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为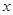 轴正半轴建立
轴正半轴建立
平面直角坐标系,直线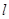 的参数方程为
的参数方程为 (
( 为参数)
为参数)
(1)把曲线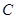 的极坐标方程化为直角坐标方程,把直线
的极坐标方程化为直角坐标方程,把直线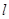 的参数方程化为普通方程;
的参数方程化为普通方程;
(2)求直线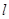 被曲线
被曲线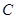 截得的线段
截得的线段 的长.
的长.
已知抛物线的顶点在原点,对称轴为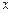 轴,抛物线上一点
轴,抛物线上一点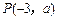 到焦点的距离为5,求抛物线的标准方程.
到焦点的距离为5,求抛物线的标准方程.
求以原点为顶点,坐标轴为对称轴,并且经过点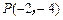 的抛物线的标准方程.
的抛物线的标准方程.
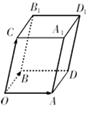
如图,已知向量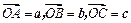 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若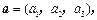
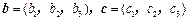 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算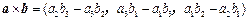 ,显然
,显然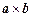 的结果仍为一向量,记作
的结果仍为一向量,记作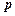 .
.
(1)求证:向量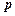 为平面
为平面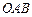 的法向量;
的法向量;
(2)求证:以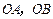 为边的平行四边形
为边的平行四边形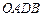 的面积等于
的面积等于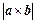 ;
;
(3)将四边形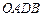 按向量
按向量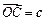 平移,得到一个平行六面体
平移,得到一个平行六面体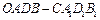 ,试判断平行六面体的体积
,试判断平行六面体的体积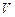 与
与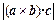 的大小.
的大小.
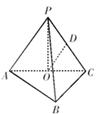
如图,在三棱锥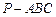 中,
中,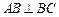 ,
,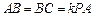 ,点
,点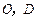 分别是
分别是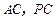 的中点,
的中点,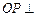 底面
底面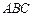 .
.
(1)求证: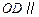 平面
平面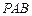 ;
;
(2)当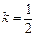 时,求直线
时,求直线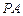 与平面
与平面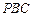 所成角的大小;
所成角的大小;
(3)当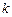 为何值时,
为何值时,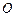 在平面
在平面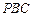 内的射影恰好为
内的射影恰好为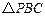 的重心?
的重心?
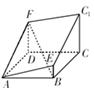
如图所示的多面体是由底面为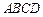 的长方体被截面
的长方体被截面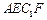 所截而得到的,其中
所截而得到的,其中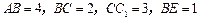 .
.
(1)求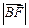 ;
;
(2)求点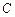 到平面
到平面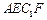 的距离.
的距离.