近年来空气污染是一个生活中重要的话题, PM2.5就是其中一个指标。PM2.5指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值在35微克/立方米以下空气质量为一级:在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.淮北相山区2014年12月1日至I0日每天的PM2.5监测数据如茎叶图所示.
(1)期间的某天小刘来此地旅游,求当天PM2.5日均监测数据未超标的概率;
(2)陶先生在此期间也有两天经过此地,这两天此地PM2.5监测数据均未超标.请计算出这两天空气质量恰好有一天为一级的概率;
(3)从所给10天的数据中任意抽取三天数据,记 表示抽到PM2.5监测数据超标的天数,求
表示抽到PM2.5监测数据超标的天数,求 的分布列及期望.
的分布列及期望.
有一块正方形 , 所在直线是一条小河,收获的蔬菜可送到 点或河边运走.于是,菜地分别为两个区域 和 ,其中 中的蔬菜运到河边较近, 中的蔬菜运到 点较近,而菜地内 和 的分界线 上的点到河边与到 点的距离相等,现建立平面直角坐标系,其中原点 为 的中点,点 的坐标为 ,如图
(1)求菜地内的分界线 的方程;
(2)菜农从蔬菜运量估计出 面积是 面积的两倍,由此得到 面积的经验值为 .设 是 上纵坐标为1的点,请计算以 为一边,另一边过点 的矩形的面积,及五边形 的面积,并判断哪一个更接近于 面积的“经验值”.

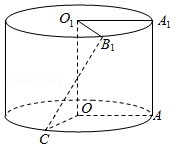
将边长为1的正方形 (及其内部)绕 旋转一周形成圆柱,如图, 长为 , 长为 ,其中 与 在平面 的同侧.
(1)求三棱锥 的体积;
(2)求异面直线 与 所成的角的大小.
已知函数 .
(1)当 时,求不等式 的解集;
(2)设函数 ,当 时, ,求 的取值范围.
在直角坐标系 中,曲线 的参数方程为 为参数),以坐标原点为极点,以 轴的正半轴为极轴,建立极坐标系,曲线 的极坐标方程为 .
(1)写出 的普通方程和 的直角坐标方程;
(2)设点 在 上,点 在 上,求 的最小值及此时 的直角坐标.
如图, 中 的中点为 ,弦 , 分别交 于 , 两点.
(1)若 ,求 的大小;
(2)若 的垂直平分线与 的垂直平分线交于点 ,证明: .
