有一块正方形 , 所在直线是一条小河,收获的蔬菜可送到 点或河边运走.于是,菜地分别为两个区域 和 ,其中 中的蔬菜运到河边较近, 中的蔬菜运到 点较近,而菜地内 和 的分界线 上的点到河边与到 点的距离相等,现建立平面直角坐标系,其中原点 为 的中点,点 的坐标为 ,如图
(1)求菜地内的分界线 的方程;
(2)菜农从蔬菜运量估计出 面积是 面积的两倍,由此得到 面积的经验值为 .设 是 上纵坐标为1的点,请计算以 为一边,另一边过点 的矩形的面积,及五边形 的面积,并判断哪一个更接近于 面积的“经验值”.

(本小题满分13分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且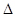 APB面积的最大值为2
APB面积的最大值为2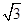 .
.
(1)求椭圆C的方程及离心率;
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.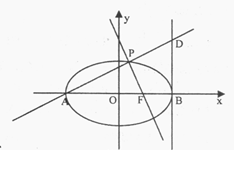
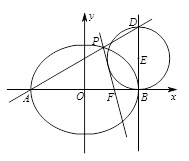
(本小题满分13分)已知四棱锥 中,
中, ,底面
,底面 是边长为
是边长为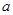 的菱形,
的菱形, ,
,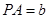 .
.
(Ⅰ)求证: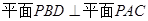 ;
;
(Ⅱ)设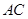 与
与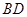 交于点
交于点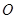 ,
, 为
为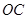 中点,若二面角
中点,若二面角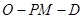 的正切值为
的正切值为 ,求
,求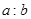 的值.
的值.
(本小题满分13分)某工厂生产A,B两种型号的玩具,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种玩具各100件进行检测,检测结果统计如下:
| 测试指标 |
[70,76) |
[76,82) |
[82,88) |
[88,94) |
[94,100) |
| 玩具A |
8 |
12 |
40 |
32 |
8 |
| 玩具B |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计玩具A、玩具B为正品的概率;
(Ⅱ)生产一件玩具A,若是正品可盈利40元,若是次品则亏损5元;生产一件玩具B,若是正品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件玩具A和1件玩具B所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件玩具B所获得的利润不少于140元的概率.
(本小题满分13分)已知向量  ,记
,记
(Ⅰ)若  ,求
,求  的值;
的值;
(Ⅱ)将函数  的图象向右平移
的图象向右平移  个单位得到
个单位得到  的图象,若函数
的图象,若函数  在
在  上有零点,求实数k的取值范围.
上有零点,求实数k的取值范围.
(本大题15分)设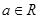 ,函数
,函数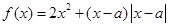 .
.
(1)当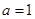 时,试解不等式
时,试解不等式 ;
;
(2)若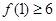 ,试求实数
,试求实数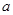 的取值范围;
的取值范围;
(3)试求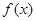 的最小值,并用
的最小值,并用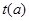 表示.
表示.