（本小题满分13分）甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
（1）用茎叶图表示这两组数据；
（2）现要从中选派一人参加数学竞赛，从统计学的角度（在平均数、方差或标准差中选两个）考虑，你认为选派哪位学生参加合适？请说明理由．
已知函数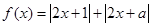 
(Ⅰ)a=-3时，求不等式 
的解集；
(Ⅱ)若关于x的不等式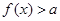 
恒成立，求实数a的取值范围
在直角坐标系中，以原点为极点，x轴的正半辐为极轴建立极坐标系，已知曲线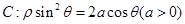
，过点P(-2，-4)的直线 
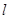的参数方程为：
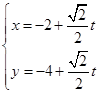（t为参数），直线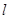与曲线C相交于M，N两点．
(Ⅰ)写出曲线C的直角坐标方程和直线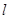的普通方程；
(Ⅱ)若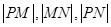
成等比数列，求a的值
如图，四边形ABCD是边长为a的正方形，以D为圆心，DA为半径的圆弧与以BC为直径的半圆O交于点C、F，连接CF并延长交AB于点E．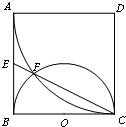
(Ⅰ)求证：E是AB的中点。
(Ⅱ)求线段BF的长．
设函数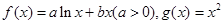 
(Ⅰ)若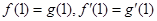
，是否存在k和m，使得 
，
，若存在，求出k和m的值，若不存在，说明理由
(Ⅱ)设 
有两个零点 
，且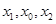 
成等差数列， 
是 G (x)的导函数，求证：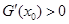 
已知椭圆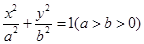 
的离心率为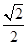 
，且过点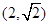 
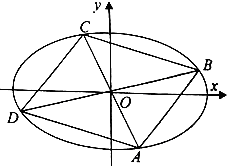
(Ⅰ)求椭圆的标准方程；
(Ⅱ)四边形ABCD的顶点在椭圆上，且对角线AC、BD过原点O，若 
．
(i)求 
的最值：
（i i）求证：四边形ABCD的面积为定值．