某软件公司新开发一款学习软件,该软件把学科知识设计为由易到难共12关的闯关游戏.为了激发闯关热情,每闯过一关都奖励若干慧币(一种网络虚拟币).该软件提供了三种奖励方案:第一种,每闯过一关奖励40慧币;第二种,闯过第一关奖励4慧币,以后每一关比前一关多奖励4慧币;第三种,闯过第一关奖励0.5 慧币,以后每一关比前一关奖励翻一番(即增加1倍),游戏规定:闯关者须于闯关前任选一种奖励方案.
(Ⅰ)设闯过n ( n∈N,且n≤12)关后三种奖励方案获得的慧币依次为 ,
, ,
, ,试求出An,
,试求出An, ,
, 的表达式;
的表达式;
(Ⅱ)如果你是一名闯关者,为了得到更多的慧币,你应如何选择奖励方案?
已知双曲线
,
为
上的任意点.
(1)求证:点
到双曲线
的两条渐近线的距离的乘积是一个常数;
(2)设点
的坐标为
,求
的最小值.
如图,某住宅小区的平面图呈圆心角为 的扇形 ,小区的两个出入口设置在点 及点 处,且小区里有一条平行于 的小路 ,已知某人从 沿 走到 用了10分钟,从 沿 走到 用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径 的长(精确到1米).

如图,在棱长为2的正方体 中, 是 的中点,求直线 与平面 所成角的大小(结果用反三角函数表示).

如图,已知点 在正方体 的对角线 上, .
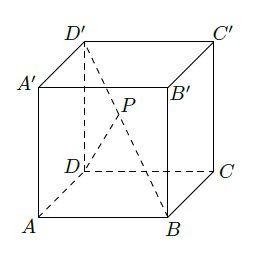
(Ⅰ)求
与
所成角的大小;
(Ⅱ)求DP与平面
所成角的大小.
已知函数
(1)若 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)若 ,证明:
,证明: