某工厂生产一种产品的原材料费为每件40元，若用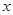
表示该厂生产这种产品的总件数，则电
力与机器保养等费用为每件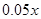
元，又该厂职工工资固定支出12500元。
（1）把每件产品的成本费
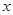（元）表示成产品件数的函数，并求每件产品的最低成本费；
（2）如果该厂生产的这种产品的数量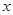不超过3000件，且产品能全部销售，根据市场调查：每件产品的
销售价
与产品件数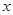有如下关系：
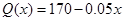，试问生产多少件产品，总利润最高？总利润
最高为多少？（总利润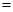
总销售额
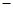总成本）
设抛物线
的焦点为
，准线为
，
，以
为圆心的圆与相切于点
，的纵坐标为
，
是圆与
轴除外的另一个交点.
(I)求抛物线
与圆的方程；
( II)已知直线
，
与交于
两点，与交于点
,且
， 求
的面积．
如图，在直三棱柱
中，D、E分别为
、AD的中点，F为
上的点，且
(I)证明：EF∥平面ABC；
(Ⅱ)若
，
，求二面角
的大小.
（在数学趣味知识培训活动中，甲、乙两名学生的6次培训成绩如下茎叶图所示：
(Ⅰ)从甲、乙两人中选择1人参加数学趣味知识竞赛，你会选哪位？请运用统计学的知识说明理由；
(II)从乙的6次培训成绩中随机选择2个，记被抽到的分数超过115分的个数为
，试求的分布列和数学期望．
已知等差数列
中，
；
是
与
的等比中项．
(I)求数列的通项公式：
(II)若
．求数列
的前
项和.
已知定义在
上的函数
，其中
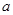为常数.
（1）当
是函数
的一个极值点，求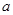的值；
（2）若函数在区间
上是增函数，求实数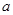的取值范围；
（3）当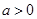
时，若
，在
处取得最大值，求实数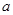的取值范围.