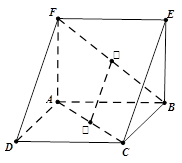
如图,三棱柱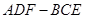 中,
中,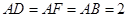 ,
, ,
,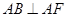 ,平面
,平面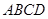 ⊥平面
⊥平面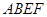 ,
, 分别是
分别是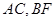 上的中点.求直线
上的中点.求直线 与平面
与平面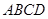 所成角( )
所成角( )
A. |
B. |
C.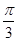 |
D. |
若集合A={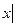 -2<
-2<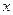 <1},B={
<1},B={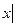 0<
0<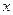 <2}则集合A∩B=()
<2}则集合A∩B=()
A.{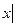 -1< -1<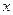 <1} <1} |
B.{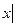 -2< -2<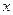 <1} <1} |
C.{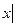 -2< -2<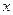 <2} <2} |
D.{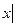 0< 0<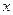 <1} <1} |
对于具有相同定义域D的函数
和
,若存在函数
为常数),对任给的正数
,存在相应的
,使得当
且
时,总有
则称直线
为曲线
与的
"分渐近线"。给出定义域均为
的四组函数如下:
①
;②
;
③
;④
.
其中,曲线
与
存在"分渐近线"的是
| A. | ①④ | B. | ②③ | C. | ②④ | D. | ③④ |
对于复数 ,若集合 具有性质"对任意 ,必有 ",则当 时, 等于
| A. | 1 | B. | -1 | C. | 0 | D. |
设不等式组 所表示的平面区域是 ,平面区域 与 关于直线 对称。对于 中的任意点 与 中的任意点 , 的最小值等于()
| A. | B. | C. | D. |
若点 和点 (-2,0)分别为双曲线 的中心和左焦点,点 为双曲线右支上的任意一点,则 的取值范围为
| A. | B. | C. | D. |