(本小题满分13分)已知抛物线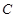 的顶点在坐标原点,焦点在正半轴上,抛物线上的点
的顶点在坐标原点,焦点在正半轴上,抛物线上的点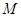 到的距离为2,且
到的距离为2,且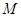 的横坐标为1.过焦点作倾斜角为锐角的直线
的横坐标为1.过焦点作倾斜角为锐角的直线 交抛物线于
交抛物线于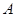 、
、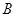 两点,且与其准线交于点
两点,且与其准线交于点 .
.
(Ⅰ)求抛物线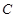 的方程;
的方程;
(Ⅱ)若线段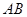 的长为
的长为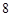 ,求直线
,求直线 的方程;
的方程;
(Ⅲ)在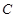 上是否存在点
上是否存在点 ,使得对任意直线
,使得对任意直线 ,直线
,直线 ,
,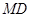 ,
,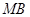 的斜率始终满足
的斜率始终满足 ,若存在求点的坐标;若不存在,请说明理由.
,若存在求点的坐标;若不存在,请说明理由.
设p:实数x满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(Ⅰ)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;

(Ⅱ)若 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
在一次模拟射击游戏中,小李连续射击了两次,设命题 :“第一次射击中靶”,命题
:“第一次射击中靶”,命题 :“第二次射击中靶”,试用
:“第二次射击中靶”,试用 ,
, 及逻辑连结词“或”“且”“非”表示下列命题:
及逻辑连结词“或”“且”“非”表示下列命题:
(1)两次射击均中靶; (2)两次射击均未中靶;

(3)两次射击恰好有一次中靶;(4)两次射击至少有一次中靶.
(本小题满分15分)已知函数,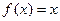 ,
,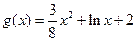 .
.
(Ⅰ)求函数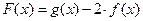 的极大值点与极小值点; (Ⅱ)若函数
的极大值点与极小值点; (Ⅱ)若函数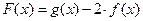 在
在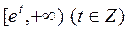 上有零点,求
上有零点,求 的最大值(
的最大值(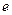 为自然对数的底数); (Ⅲ)设
为自然对数的底数); (Ⅲ)设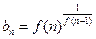 (
(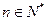 ),试问数列
),试问数列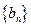 中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由.
中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由.
(本小题满分14分)在平面直角坐标系中,O为坐标原点,已知向量 又点
又点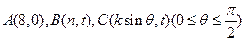 . (Ⅰ)若
. (Ⅰ)若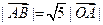 且
且 , 求向量
, 求向量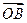 ; (Ⅱ)若向量
; (Ⅱ)若向量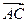 与向量
与向量 共线,当k
共线,当k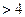 ,且
,且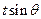 取最大值4时,求
取最大值4时,求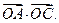
(本小题满分15分)已知数列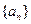 中,
中,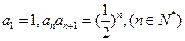 .
.
(Ⅰ)求证:数列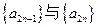 (
(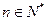 )均为等比数列; (Ⅱ)求数列
)均为等比数列; (Ⅱ)求数列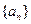 的前
的前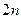 项和
项和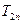 ; (Ⅲ)若数列
; (Ⅲ)若数列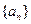 的前
的前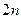 项和为
项和为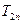 ,不等式
,不等式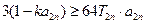 对
对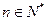 恒成立,求
恒成立,求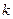 的最大值.
的最大值.